Нормальный закон распределения случайных величин.

Нормальный закон распределения (закон Гаусса) играет осо­бо важную роль в теории вероятностей и чаще других применяется в решении практических задач. Его главная особенность в том, что он является предельным законом, к которому приближаются дру­гие законы распределения при весьма часто встречающихся типич­ных условиях. Например, сумма достаточно большого числа неза­висимых (или слабо зависимых) случайных величин приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем больше случайных величин суммируется.

Экспериментально доказано, что нормальному закону под­чиняются погрешности измерений, отклонения геометрических размеров и положения элементов строительных конструкций при их изготовлении и монтаже, изменчивость физико-механических характеристик материалов и нагру­зок, действующих на строительные конструкции.

Распределению Гаусса подчи­няются почти все случайные вели­чины, отклонение которых от сред­них значений вызывается большой совокупностью случайных факто­ров, каждый из которых в отдельности незначителен (центральная предельная теорема).

Нормальным распределением называется распределение случайной непрерывной величины, для которых плотность вероят­ностей имеет вид (рис. 18.1).

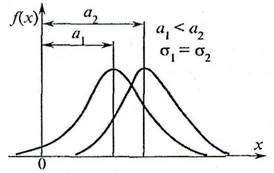
Рис. 18.1. Нормальный закон распределения при а₁ < a₂.

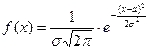
где а и 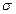— параметры распределения.

Вероятностные характеристики случайной величины, распре­деленной по нормальному закону, равны:

• математическое ожидание 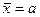(18.2)

• дисперсия 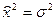(18.3)

• среднеквадратичное отклонение 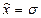(18.4)

• коэффициент асимметрии А = 0 (18.5)

• эксцесс Е = 0. (18.6)

Параметр σ, входящий в распределение Гаусса равен сред­неквадратичному отношению слу­чайной величины. Величина а оп­ределяет положение центра рас­пределения (см. рис. 18.1), а величина а—ширину распределе­ния (рис. 18.2), т.е. статистический разброс вокруг средней величины.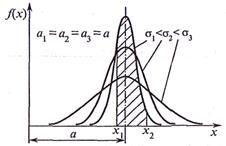

Рис. 18.2. Нормальный закон распределения при σ₁ < σ₂ < σ₃

Вероятность попадания в заданный интервал (от x₁ до x₂) для нормального распределения, как и во всех случаях, определяется интегралом от плотности вероятности (18.1), который не выража­ется через элементарные функции и представляется специальной функцией, называется функцией Лапласа (интеграл вероятностей).

Одно из представлений интеграла вероятностей:

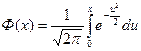(18.7)

где

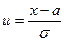(18.8)

Величина и называется квантилем.

Видно, что Ф(х)— нечетная функция, т. е. Ф(-х) = -Ф(х). Значения этой функции вычислены и представлены в виде таблиц в технической и учебной литературе.

Функция распределения нормального закона (рис. 18.3) может быть выражена через ин­теграл вероятностей:

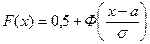(18.9)

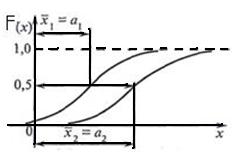
Рис. 18.2. Функция нормального закона распределения.

Вероятность попадания случайной величины, распределенной по нормальному закону, в интервал от х. до х, определяется выра­жением:

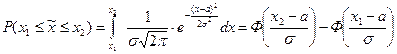(18.10)

Следует заметить, что

Ф(0) = 0; Ф(∞) = 0,5; Ф(-∞) = -0,5.

При решении практических задач, связанных с распределе­нием, часто приходится рассматривать вероятность попадания в интервал, симметричный относительно математического ожидания, если длина этого интервала 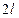т.е. если сам интервал имеет грани­цу от 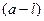до 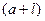, имеем:

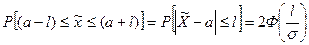(18.11)

При решении практических задач границы отклонений слу­чайных величин выражаются через стандарт, среднеквадратичное отклонение, умноженное на некоторый множитель, определяющий границы области отклонений случайной величины.

Принимая 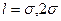и 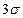а также используя формулу (18.10) и таблицу Ф(х) (приложение № 1), получим

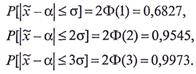
Эти формулы показывают, что если случайная величина име­ет нормальное распределение, то вероятность ее отклонения от сво­его среднего значения не более чем на σ составляет 68,27 %, не бо­лее чем на 2σ — 95,45 % и не более чем на Зσ — 99,73 %.

Поскольку величина 0,9973 близка к единице, практически считается невозможным отклонение нормального распределения случайной величины от математического ожидания более чем на Зσ. Это правило, справедливое только для нормального распределения, называется правилом трех сигм. Нарушение его имеет вероятность Р = 1 - 0,9973 = 0,0027. Этим правилом пользуются при установле­нии границ допустимых отклонений допусков геометрических ха­рактеристик изделий и конструкций.