Законы распределения случайных величин.
Случайная величина (СВ) - это изменчивая величина, которая может принимать то или иное значение в зависимости от степени воздействия на нее случайных факторов. Численное значение случайной величины предсказать трудно. Тем не менее практически важно знать, какое из возможных численных значений и с какой вероятностью может принять случайная величина в результате случайного события. Случайные величины могут быть дискретными (прерывными) и непрерывными.
Дискретная случайная величина (ДСВ) принимает только отдельные, изолированные возможные значения с определенными вероятностями. Чаще всего дискретные величины принимают только целые значения, тогда их называют целочисленными.
Примеры дискретных случайных величин:
• число циклов повторной нагрузки до разрушения конструкции;
• число дефектных изделий (панелей) в партии;
• число станков, требующих подналадки.
ДСВ считается известной, если известны принимаемые ею значения и вероятности. Для ДСВ распределение вероятностей представляет собой совокупность вероятностей случайных событий, заключающихся в том, что СВ принимает одно из возможных значений. Формула для распределения вероятностей ДСВ в общем случае имеет вид:
| (17.1) |
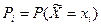
где 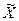 — случайная дискретная величина,
— случайная дискретная величина,
хi — возможные значения ДСВ, i= 1,2,3...п
Правая часть равенства (17.1) означает вероятность того, что ДСВ примет значение х.. Закон распределения ДСВ согласно (17.1) записывается в виде таблицы (табл. 17.1).
Распределение случайной дискретной величины Таблица 17.1
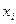
| 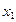
| 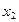
| 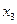
| … | 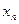
|
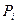
| 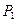
| 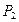
| 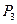
| … | 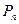
|
Сумма Р, как сумма вероятностей группы несовместимых событий должна быть равна единице:
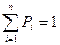
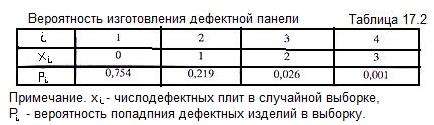
Пример 17.1. Завод изготавливает железобетонные панели. Если из большой партии отобрать три изделия, то возможные значения дефектных панелей в случайной выборке будут равны 0, 1,2,3. На основе наблюдений и измерений установлены вероятности попаданий дефектных изделий в случайную выборку (табл.17.2).
Рассмотренные четыре вероятности образуют распределение вероятностей ДСВ — числа дефектных плит в случайной выборке. Контроль:
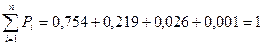
Анализируя данные табл. 17.2 и учитывая статистический характер вероятности, можно предполагать, что при большем количестве выборок по три плиты каждая согласно закону больших чисел примерно 75 % выборок не будут иметь ни одного дефектного изделия, 22 %—одно, 3 %—два и 0,1 %—все три, т.е. в последнем случае в одной из тысячи выборок все три изделия окажутся дефектными.
Данные о вероятностях и значениях ДСВ из табл. 17. 2 можно представить в виде графика (рис. 17.1).
Иногда вершины отрезков, определяющих величину вероятностей, соединяют ломаной линией, которую часто называют многоугольником распределения.
Таким образом, закон распределения ДСВ может быть задан аналитически (17.1), в виде таблицы или графически. 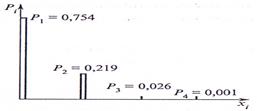
Рис. 17.1. Вероятность попадания дефектных железобетонных панелей в случайную выборку.
Непрерывная случайная величина (НСВ) принимает любые значения из непрерывного числового множества в промежутке между предельными значениями. Эти значения могут быть целыми и дробными. Очевидно, число возможных значений непрерывной величины будет бесконечно.
Примеры непрерывных случайных величин.
1) Предел текучести стали изменяется в пределах от
 |
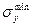 =210 МПа до
=210 МПа до 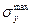 = 360 МПа. Случайные значения предела текучести будут находиться в промежутке между этими значениями
= 360 МПа. Случайные значения предела текучести будут находиться в промежутке между этими значениями 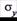 = 210...360 МПа. Количество значений предела текучести в указанных пределах будет бесконечно.
= 210...360 МПа. Количество значений предела текучести в указанных пределах будет бесконечно.
2) Срок службы деревянных конструкций складов минеральных удобрений колеблется в пределах 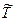 = 30...50 лет.
= 30...50 лет.
3) Прочность бетона на сжатие класса В30 может изменяться в пределах 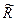 = 28...50 МПа.
= 28...50 МПа.
4) Прогибы изгибаемых элементов могут отличаться от средних значений на 15. ..20%.
5) Ширина раскрытия трещин в железобетонных конструкциях может изменяться в пределах 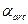 = 0,01...0,4 мм.
= 0,01...0,4 мм.
Для количественной характеристики распределения вероятностей удобно пользоваться не вероятностью события при некотором значении текущей переменной х, а вероятностью события того, что случайная величина будет меньше этого значения текущей переменной. С этой целью вводится функция распределения случайной величины.
 Функцией распределения F(x) называется функция, определяющая вероятность того, что случайная величина
Функцией распределения F(x) называется функция, определяющая вероятность того, что случайная величина 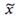 в результате испытаний примет значение меньше х:
в результате испытаний примет значение меньше х:
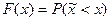
где х — текущая переменная.
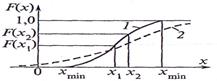
Функция распределения является самой универсальной характеристикой как для ДСВ, так и для НСВ. Функция распределения полности характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения. Функцию распределения иногда называют интегральной функцией распределения. Она может иметь конечные и бесконечные пределы (рис. 17.2)
Рис. 17.2. Функция распределения непрерывной случайной величины: 1 — при ограниченных значениях случайной величины; 2—при неограниченных значениях случайной величины.
Дата добавления: 2015-02-16; просмотров: 1414;
