Основные свойства плотности распределения

1.Плотность распределения есть неотрицательная функция:

f(x) ≥ 0

Это свойство вытекает непосредственно из того, что интег­ральная функция распределения есть неубывающая функция. Гео­метрически это свойство означает, что точки, принадлежащие гра­фику плотности распределения, расположены над осью ОХ.

2. Интеграл от плотности распределения в пределах измене­ния НСВ равен единице:

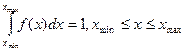
Это означает, что событие достоверно и его вероятность рав­на единице. Геометрически это означает, что вся площадь, ограни­ченная осью ОХ и кривой распределения, равна единице.

Функция F(x), как и всякая вероятность, величина безразмер­ная. Размерность плотности распределения f(х) обратна размерно­сти случайной величины.

Вероятность попадания НСВ в интервал равна определенному интегралу:

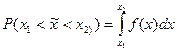
Геометрически вероятность попадания случайной величины 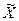на участок x₁…x₂ равна заштрихованной площади, ограниченной кривой плотностью распределения в пределах данного участка и осью абсцисс (см. рис. 17.3).

Вероятность попадания НСВ в определенный интервал мож­но вычислить также с помощью интегральной функции распреде­ления:

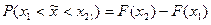
где F(x₁) и F(x₂) значение интегральной функции распределения на границах интервала.

Примеры законов распределения непрерывной случайной ве­личины.

1) Нормальный закон распределения

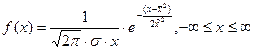
2) Логарифмически нормальный

3) Экспоненциальное распределение

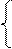
где 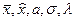- параметры распределений, получаемые на основе статистической обработки экспериментальных данных.