Общие свойства интегральной функции распределения
1. Функция F(x) есть неубывающая функция своего аргумента:
F(x2 )> F(x1) при x2 > x1
2. Интегральная функция распределения изменяется в пределах
от 0 до 1.
3. Если возможные значения случайной величины конечны (см. рис. 17.2, кривая 1), то
F(x) = 0 при x1 ≤ xmin
F(x) = 1 при x1 ≥ xmax
Если возможные значения непрерывной случайной величины расположены по всей оси х (см. рис.17.2, кривая 2), то справедливы следующие предельные соотношения:
F(x) = 0 при х = -∞
F(x) = 1 при x = ∞
НСВ можно задать, используя другую функцию, которую называют плотностью распределения, или плотностью вероятности (иногда ее называют дифференциальной функцией).
Плотностью распределения НСВ называют первую производную от интегральной функции распределения:
f(x) = F/(x)
Дифференциальную функцию распределения НСВ удобно представить в графической форме (рис. 17.3).
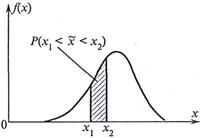 |
Рис. 17.3. Плотность распределения непрерывной случайной величины.
Дата добавления: 2015-02-16; просмотров: 1048;
