Развитие методов расчетной оценки безопасной работы строительных конструкций.
Главной задачей расчета несущих конструкций является создание определенных гарантий обеспечения нормальной и безопасной работы конструкции в течение расчетного срока службы сооружения. Поставленная цель должна быть достигнута при минимальных расходах материалов, энергии, трудовых затрат и обеспечении высоких эксплутационных качеств здания или сооружения. Гарантии безопасной работы окончательно устанавливаются на заключительном этапе расчета, когда сопоставляют усилия от внешних нагрузок (воздействий) с несущей способностью конструкции.
С развитием методов расчета совершенствовались критерии оценок гарантий безопасной работы конструкций.
| (15.1) |
1. Оценка безопасной работы конструкции с применением раздельных коэффициентов запаса для каждого конструкционного материала. Эти критерии применяются при расчете по методу допускаемых напряжений, в основу которого положена теория упругого деформирования. При расчете определялись напряжения в бетоне и арматуре σb и σs и сравнивались с допускаемыми: 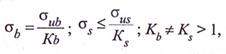
где σub и σus — предел прочности бетона на сжатие и предел текучести арматуры на растяжение;
Кb и Кs — коэффициенты запаса по прочности бетона на сжатие и предела текучести арматуры на растяжение.
Оценка безопасной работы конструкции с помощью раздельных коэффициентов запаса Кb и Кs является приближенной.
В основу расчета строительных конструкций по допускаемым напряжениям положены формулы сопротивления материалов для упругих материалов.
Коэффициенты запаса для каждого материала устанавливают в зависимости от характера действующих усилий с учетом несоответствия расчетной схемы действительной работе конструкции, возможного превышения нагрузок, отклонения размеров сооружений от проектных и т.д.
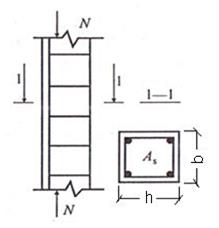
Рис. 15.1. Работа железобетонного элемента на сжатие.
Расчет металлических и деревянных конструкций проводят как для однородных материалов. В железобетонных конструкциях учитывают совместную работу бетона и арматуры вследствие наличия между ними сцепления, а также возможность образования трещин в бетоне при растягивающих
напряжениях.
Так, в сжатых железобетонных элементах с площадью бетона Ab= bh и площадью арматуры As (рис. 15.1) вследствие равенства относительных деформаций бетона εb, и арматуры εs:
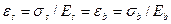 (15.2)
(15.2)
напряжения арматуры и бетона находятся в соотношении
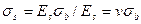 (15.3)
(15.3)
где
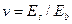 (15.4)
(15.4)
Еs и Еb. — модули упругости арматуры и бетона.
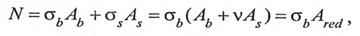 |
Сила сжатия N , воспринимаемая элементом (см. рис. 15.1):
где Ared — приведенная площадь, Ared =Ab+ νAs.
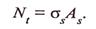 |
В растянутых железобетонных элементах до образования трещин расчет ведут по этим же формулам; после образования трещин все усилия растяжения Nt сечении элемента с трещиной воспринимает только арматура и расчетная формула имеет вид:
При расчете изгибаемых железобетонных элементов принимают, что бетон в растянутой зоне не участвует в работе. Эпюру напряжений в сжатой зоне принимают треугольной.
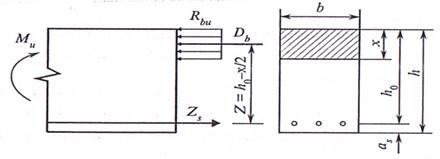
На рис. 15.2 показана схема усилий в изгибаемом железобетонном элементе прямоугольного поперечного сечения при расчете по допускаемым напряжениям.
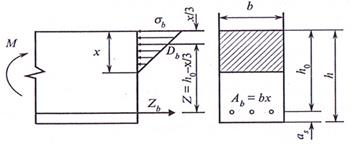
Рис. 15.2. Схема усилий в изгибаемом железобетонном элементе прямоугольного поперечного сечения при расчете по допускаемым напряжениям.
Действующий в нормальном сечении элемента момент М от внешних нагрузок воспринимается внутренними усилиями Zs = Db с плечом zb = h0 - x/3,
где Zs — равнодействующая усилий в растянутой арматуре;
Db — то же в сжатом бетоне; х — высота сжатой зоны.
Напряжения в бетоне и арматуре определяют по формулам:
| (15.5) |
| (15.6) |
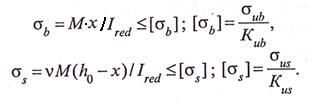
Значение х находят из условия равенства нулю статического момента приведенной площади сечения относительно нейтральной оси
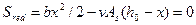 (15.7)
(15.7)
Момент инерции приведенного сечения
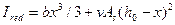 (15.8)
(15.8)
Внецентренно нагруженные железобетонные элементы рассчитывают по формуле:
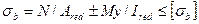 (15.9)
(15.9)
где N и M — нормальная сила и момент от внешних усилий;
у — расстояние от нейтральной оси сечения до кромки, при которой определяют напряжение.
 Расчет по допускаемым напряжениям производят для элементов по их состоянию в период эксплуатации. Этот метод не учитывает пластические деформации бетона и арматуры, что ведет к неоправданному перерасходу материалов. Величина v для железобетонных конструкций не является постоянной, что также не учитывается. Для железобетонных конструкций неизвестен об- щий коэффициент запаса.
Расчет по допускаемым напряжениям производят для элементов по их состоянию в период эксплуатации. Этот метод не учитывает пластические деформации бетона и арматуры, что ведет к неоправданному перерасходу материалов. Величина v для железобетонных конструкций не является постоянной, что также не учитывается. Для железобетонных конструкций неизвестен об- щий коэффициент запаса.
Расчет по допускаемым напряжениям дает возможность только весьма приближенно оценить величину напряжений, возникающих в конструкциях в стадии эксплуатации. Этот метод расчета, несмотря на его недостатки, до настоящего времени применяется в некоторых зарубежных странах. Отдельные положения расчета по допускаемым напряжениям практикуются и у нас при расчетах предварительно напряженных железобетонных элементов.
2. Оценка безопасной работы конструкции с помощью единого коэффициента запаса конструкции К.. Расчет производится по методу разрушающих усилий и вместо гипотезы плоских сечений применяется принцип пластического разрушения. В расчете учитываются пластические деформации. Гарантии безопасной работы устанавливаются путем сравнения момента М (или усилия) от эксплуатационной нагрузки с несущей способностью, отнесенной к единому коэффициенту запаса К:
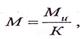
где Ми — несущая способность элемента.
При разрушении железобетонного изгибаемого элемента напряжение в растянутой арматуре достигает предела текучести σу, а в сжатом бетоне — предела прочности Rbu.
В стадии разрушения изгибаемого элемента очертание эпюры напряжений бетона сжатой зоны близко к параболе 3-й степени, которую для упрощения расчетных формул заменяют прямоугольником (рис. 15.3).
Рис. 15.3. Схема усилий в изгибаемом элементе прямоугольного сечения при расчете по разрушающим усилиям.
Погрешность, которую дает такое упрощение при определении изгибающего момента, при малых и средних процентах армирования незначительна (1...2 %).
Расчет на изгиб любого сечения, симметричного относительно вертикальной оси, производится исходя из двух условий статики.
•проекции всех сил на нейтральную ось равна нулю:
ΣN = 0; (15.10)
•сумма моментов всех сил относительно центра тяжести растянутой арматуры равна нулю:
ΣМ = 0. (15.11)
Из условия (15.10) определяют положение нейтральной оси. Например, для прямоугольного сечения:
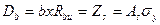
Отсюда
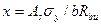
По условию (15.11) определяют величину разрушающего момента. Для прямоугольного сечения:
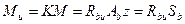 (15.12)
(15.12)
где Sb=AbZ— статический момент сжатой зоны относительно центра растянутой арматуры.
Достоинством расчета по разрушающим усилиям является то, что он учитывает упругопластические свойства железобетона, дает экономию арматуры по сравнению с расчетом по допускаемым напряжениям. Введение единого коэффициента запаса К по усилиям дает возможность оценить надежность конструкции.
В настоящее время формулы расчета на прочность по разрушающим усилиям применяют при испытании новых типов конструкции до разрушения. При этом в расчет вводят прочностные характеристики бетона и арматуры, полученные в результате испытаний контрольных образцов.
Существенным недостатком метода расчета по разрушающим усилиям является то, что единый коэффициент запаса К лишь приблизительно учитывает изменчивость нагрузок, прочностных характеристик бетона и арматуры, условия изготовления и работы конструкций, что в отдельных случаях это ведет к перерасходу материала или не обеспечивает достаточной надежности конструкций. Напряженное состояние в период эксплуатации не контролируется. Поэтому коэффициент К получил меткое название «коэффициент незнания».
3. Оценка работы конструкции с помощью частных коэффициентов запаса. Такая оценка применяется при расчете по методу предельных состояний. Главное отличие состоит в том, что вместо единого коэффициента запаса вводится система частных коэффициентов, каждый из которых раздельно оценивает случайные параметры нагрузок, прочностных свойств материалов, условий воздействия и работы конструкции. Гарантии безопасной работы конструкции записываются в виде главного неравенства метода предельных состояний:
| (15.13) |
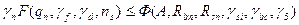
γn, γf, γbc, γ5— коэффициенты надежности соответственно по назначению, нагрузке, бетону, арматуре;
ns и γn— коэффициент сочетаний нагрузок и коэффициент условий работы конструкции;
qп, Rbn, Rsn — нормативная нагрузка, нормативное сопротивление бетона и арматуры;
А — геометрический фактор.
Левая часть неравенства (15.13) представляет собой усилие от расчетных нагрузок, правая — несущую способность.
Оценка безопасной работы конструкции с помощью частных коэффициентов запаса не учитывает в явном виде фактор времени. При таком подходе неясен срок службы конструкции, а фактор времени выпадает из оценки эксплуатационных качеств конструкции и ее прочностных и деформативных показателей. По существу устанавливается безопасность только что изготовленной конструкции, а не конструкции, которой предстоит воспринимать нагрузку в течение длительного времени.
4. Оценка безопасной работы конструкции с применением
вероятностных показателей. В основе вероятностного расчета конструкции лежат представления о том, что нагрузки и поведение конструкции являются случайными процессами, развертывающимися во времени, а надежность конструкции отождествляется с вероятностью ее нахождения в пределах допускаемой области. Гарантии безопасной роботы конструкции формулируются в следующем виде:
| (15.14) |
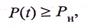
где P(t), Pн— вероятность надежной работы конструкции и ее нормативное значение.
Вероятностный метод расчета согласно (15.14) является наиболее обоснованным, отражающим природу случайного характера поведения конструкции.
К недостаткам метода относятся:
• сложность контроля напряженного состояния в процессе эксплуатации;
• абстрактный характер показателей надежности, трудность понимания практического аспекта его применения;
• неизвестность остаточного срока службы конструкции и затруднение его рекомендации с учетом фактического состояния режима эксплуатации после реконструкции объекта.
5. Оценка безопасной работы конструкции на основе расчетов сроков ее службы. Срок службы конструкции определяется с учетом изменений нагрузки и несущей способности во времени, случайных параметров, определяющих поведение конструкции в процессе-эксплуатации. Гарантия безопасной работы конструкции устанавливается на основе следующего неравенства:
| (15.15) |
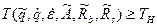
где 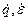 — скорости изменения нагрузки и деформаций с течением времени;
— скорости изменения нагрузки и деформаций с течением времени;
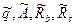 —случайные значения нагрузки, геометрических размеров, прочностных характеристик бетона и арматуры.
—случайные значения нагрузки, геометрических размеров, прочностных характеристик бетона и арматуры.
Левая часть неравенства (15.15) представляет собой срок службы конструкции с заданной вероятностью, правая — его нормативное значение Тн.
Из приведенных критериев оценки гарантии безопасной работы конструкции наиболее целесообразным, отражающим реальную ценность конструкции, ее способность выполнять главное функциональное назначение по восприятию действующих нагрузок, является срок службы. Расчеты строительных конструкций с определением сроков службы, развиваемые в последнее время, весьма перспективны.
Дата добавления: 2015-02-16; просмотров: 1514;
