Лекция 14. Конвекция. Ламинарный и турбулентный режимы течения. Основные уравнения теории конвективного теплообмена.

Конвекция - это процесс теплопередачи, осуществляемый путем переноса энергии потоками жидкости или газа. Явление конвекции можно объяснить законом Архимеда и явлением теплового расширения тел. При повышении температуры объем жидкости возрастает, а плотность уменьшается. Под действием архимедовых сил менее плотная нагретая жидкость поднимается вверх, а более плотная холодная жидкость опускается вниз. Если же жидкость нагревать сверх, то менее плотная теплая жидкость там и останется и конвекция не возникнет. Так устанавливается круговорот жидкости, сопровождающийся переносом энергии от нагретых участков к более холодным. Совершенно аналогичным образом возникает конвекция в газах. Естественная конвекция. Для ее возникновения требуется подогрев жидкости снизу (или охлаждение сверху), причем нагрев в разных участках должен быть неравномерным. Кроме естественной конвекции, возможна и принудительная конвекция. При принудительной конвекции потоки нагретой (или охлажденной) жидкости или газа переносятся под действием насосов или вентиляторов. Такая конвекция используется в тех случаях, когда естественная конвекция оказывается недостаточно эффективной, а также в состоянии невесомости, когда естественная конвекция невозможна.

Явление возникновения струй или потоков в нагреваемых или охлаждаемых жидкостях и газах называется конвекцией. Кроме того, с точки зрения термодинамики конвекция– это способ теплопередачи, при котором внутренняя энергия переносится потоками неравномерно нагретых веществ.

Теплообмен конвекцией часто встречается в быту. Например, отопительные батареи-радиаторы располагаются вблизи пола под подоконником. Поэтому нагреваемый ими воздух, поднимаясь вверх, смешивается с холодным воздухом, опускающимся от окна. В результате в комнате устанавливается почти равномерная температура. Этого не происходило бы, если бы батареи располагались у потолка. Конвективные потоки возникают и внутри кастрюль с жидкостями, которые нагреваются на кухонной плите.

Явление конвекции весьма распространено в природе. Типичными примерами конвекции в атмосфере являются ветры, в частности бризы и муссоны. Нагреваясь над одними участками Земли и охлаждаясь над другими, воздух начинает циркулировать, перенося с собой энергию и влагу. Явление это весьма сложное. На процесс естественной конвекции накладывается ряд факторов, в частности суточное вращение Земли, рельеф местности, влияние морских течений и т. д. Но в основе ветрообразования лежит именно явление конвекции. Особенно прост и нагляден механизм возникновения берегового бриза. Днем суша прогревается быстрее воды, у которой теплоемкость очень велика. Поэтому температура суши выше температуры воды. Нагретый над сушей воздух поднимается вверх, на его место поступает холодный воздух с моря, и у поверхности Земли ветер дует с моря на берег. Ночью картина меняется на противоположную: земля быстрее остывает, вода сохраняет более высокую температуру, и ветер у поверхности Земли направлен в сторону моря.

С явлением конвекции связаны процессы горообразования, процессы парения птиц и планеров, процесс дымообразования из труб и кратеров вулканов, охлаждение продуктов в холодильнике.

Ламинарное течение (от лат. lamina — пластинка), упорядоченное течение жидкости или газа, при котором жидкость или газ перемещается как бы слоями, параллельными направлению течения. Ламинарное течение наблюдается или у очень вязких жидкостей, или при течениях, происходящих с достаточно малыми скоростями, а также при медленном обтекании жидкостью тел малых размеров. В частности, ламинарное течение имеет место в узких (капиллярных) трубках, в слое смазки в подшипниках, в тонком пограничном слое, который образуется вблизи поверхности тел при обтекании их жидкостью или газом, и др. С увеличением скорости движения данной жидкости ламинарное течение может в некоторый момент перейти в неупорядоченное турбулентное течение. При этом резко изменяется сила сопротивления движения. Режим течения жидкости характеризуется числом Рейнольдса Re. Когда значение Re меньше некоторого критического числа Re_kp, имеет место Ламинарному течению жидкости; если Re > Re_kp, режим течения может стать турбулентным. Значение Rе_кр зависит от вида рассматриваемого течения. Так, для течения в круглых трубах Rе_кр  2200 (если характерной скоростью считать среднюю по сечению скорость, а характерным размером — диаметр трубы). Следовательно, при Re_kp < 2200 течение жидкости в трубе будет ламинарным.

Турбулентное течение(от лат. turbulentus — бурный, беспорядочный), форма течения жидкости или газа, при которой их элементы совершают неупорядоченные, неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями движущихся жидкости или газа.

Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой жидкости в трубах.

Обычно турбулентность наступает при превышении некоторого критического числа Рейнольдса или Релея (в частном случае скорости потока при постоянной плотности и диаметре трубы или температуры на внешней границе среды).

Турбулентность, например, можно создать:

· увеличив число Рейнольдса (увеличить линейную скорость или угловую скорость вращения потока, размер обтекаемого тела, уменьшить первый или второй коэффициент молекулярной вязкости, увеличить плотность среды) и/или число Релея (нагреть среду) и/или увеличить число Прандтля (уменьшить вязкость);

· и/или задать очень сложный вид внешней силы (примеры: хаотичная сила, удар). Течение может не иметь фрактальных свойств;

· и/или создать сложные граничные и/или начальные условия, задав функцию формы границ. Например, их можно представить случайной функцией. Например: течение при взрыве сосуда с газом;

· и/или создать квантовое состояние. Данное условие применимо только к изотопу гелия 3 и 4. Все остальные вещества замерзают, оставаясь в нормальном, не квантовом состоянии;

· облучить среду звуком высокой интенсивности;

· с помощью химических реакций, например горения. Форма пламени, как и вид водопада может быть разным.

При больших числах Рейнольдса, скорости потока от небольших изменений на границе зависят слабо. Поэтому при разных начальных скоростях движения корабля формируется одна и та же волна перед его носом, когда он движется с крейсерской скоростью. Нос ракеты обгорает и создаётся одинаковая картина разгара, несмотря на разную начальную скорость.

При очень малом числе Рейнольдса — это всем известные линейные волны на воде небольшой амплитуды. При большой скорости мы наблюдаем нелинейные волны цунами или обрушение волн прибоя. Например, крупные волны за плотиной распадаются на волны меньших размеров.

Вследствие нелинейных волн любые параметры среды: (скорость, температура, давление, плотность) могут испытывать хаотические колебания, изменяются от точки к точке и во времени непериодически. Они очень чувствительны к малейшим изменением параметров среды. В турбулентном течении мгновенные параметры среды распределены по случайному закону. Этим турбулентные течения отличаются от ламинарных течений. Но управляя средними параметрами, мы можем управлять турбулентностью.

Общепринято считать проекцию вектора скорости на ось координат в турбулентном потоке, состоящей из средней или осредненной величины, за некоторое выбранное время, и плюс мгновенной составляющей:

U = U_cp + u' = 100 м/c + 0.5 м/с.

Здесь u' — пульсационная составляющая или пульсация. Удобно оказалось ввести степень турбулентности:

e = 100%*u'/U_cp = 100 %*0.5/100 = 0,5%.

Для трех осей: e = (u' + v' + w')/U_cp.

Турбулентное течение с большим числом Рейнольдса называют развитой турбулентностью. При разных граничных условиях оно всегда приводит к созданию одного и того же профиля скоростей. Это свойство независимости параметров от числа Рейнольдса называют автомодельностью течения. Наблюдается экспериментально в струях или в пограничном слое.

Можно создать изотропную турбулентность, когда статистические параметры течения (функция распределения вероятности, дисперсия, моменты) одинаковы в направлении разных осей координат и не зависят от времени.

При процессах горения или химических реакциях на явление турбулентности накладываются множество других физических и химических процессов. Например, эффект конвекции, автоколебаний, гистерезиса. В этом случае говорят о турбулентной конвекции. Обычно принимается, что переход от ламинарного течения к турбулентному происходит при достижении критического числа Рейнольдса (Re). Критическое значение числа Рейнольдса зависит от конкретного вида течения, его коэффициента вязкости, который зависит от температуры, которое зависит от давления (течение в круглой трубе, обтекание шара и т. п.).

Конвективный теплообмен – это совместный перенос теплоты теплопроводностью и конвекцией. Конвекция может иметь место в жидкостях, газах и расплавленных металлах.

Плотность конвективного теплового потока определяется по уравнению Ньютона–Рихмана, Вт/м²:

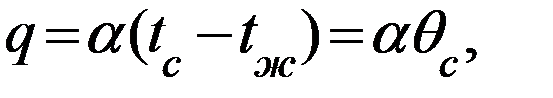14.1

где α - коэффициент конвективной теплоотдачи, Вт/м²К;

t_ct_ж - температуры стенки и жидкости, °С; Q_c - разность температур между стенкой и жидкостью, К.

В качестве теплоносителей в настоящее время применяют воздух и другие газы, воду, масла, спирты, жидкие металлы. Процесс теплоотдачи при этом существенно зависит от физических свойств теплоносителя. К ним относятся:

λ - теплопроводность, Вт/(мК); ρ - плотность, кг/м³; с - массоваятеплоемкость, Дж/(кгК); α=λ/(ρc) коэффициент температуропроводности, м²/с.

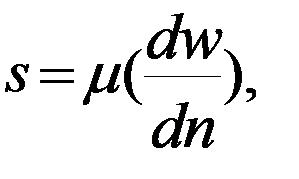Из-за вязкости жидкости, между ее слоями, движущимися с разной скоростью, возникает трение. Согласно закону Ньютона касательная сила трения, Н/м²:

где µ коэффициент динамической вязкости, размерность которого из предыдущей формулы:

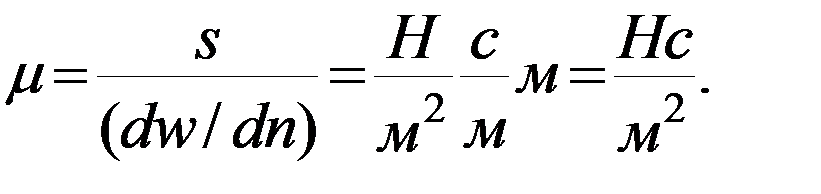
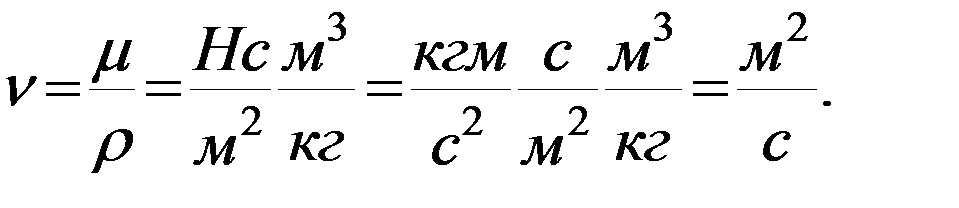Наряду с динамической вязкостью жидкости, часто используется коэффициент кинематической вязкости:

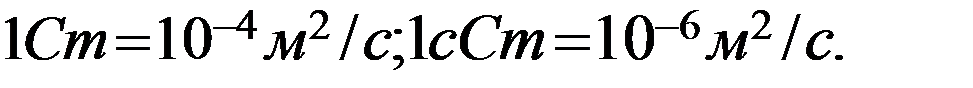До введения международной системы единиц «СИ» кинематическая вязкость измерялась в Стоксах и сантиСтоксах:

На преодоление вязкостных сил расходуется часть кинетической энергии жидкости, которая переходит в тепловую энергию (диссипация энергии). С увеличением скорости жидкости диссипация энергии возрастает.

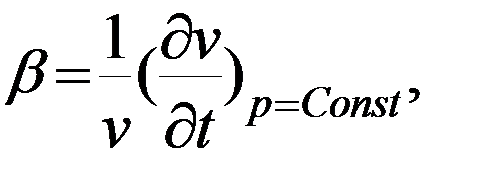При свободной (естественной) конвекции существенное значение имеет коэффициент объемного (температурного) расширения жидкости, 1/К:

то есть относительное изменение объема жидкости при увеличении ее температуры на 1 К. Для разных жидкостей значение β приводится в справочных таблицах.

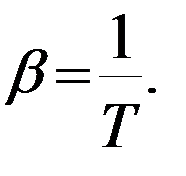Для идеальных газов его можно определить по формуле: