Основной закон теплопроводности

Для распространения теплоты в любом теле или пространстве необходимо наличие разности температур в различных точках тела. Это условие относится и к передаче теплоты теплопроводностью, при которой градиент температуры в различных точках тела не должен быть равен нулю.

Связь между количеством теплоты δQ, проходящим за промежуток времени dt через элементарную площадку dS, расположенную на изотермической поверхности, и градиентом температуры устанавливается гипотезой Фурье, согласно которой

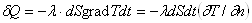.(12.1)

Минус в правой части показывает, что в направлении теплового потока температура убывает и grad T является величиной отрицательной. Коэффициент пропорциональности λ называется коэффициентом теплопроводности или более кратко теплопроводностью. Справедливость гипотезы Фурье подтверждено многочисленными опытными данными, поэтому эта гипотеза в настоящее время носит название основного уравнения теплопроводности или закона Фурье.

Отношение количества теплоты, проходящего через заданную поверхность, ко времени называют тепловым потоком. Тепловой поток обозначают q и выражают в ваттах (Вт):

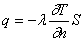(12.2)

Если относительное изменение температуры Т на расстоянии средней длины свободного пробега частиц l мало, то выполняется основной закон теплопроводности (закон Фурье): плотность теплового потока q пропорциональна градиенту температуры grad T, то есть

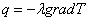(12.3)

(где λ — коэффициент теплопроводности или просто теплопроводность) Отношение теплового потока dq через малый элемент поверхности к площади dS этой поверхности называют поверхностной плотностью теплового потока (или вектором плотности теплового потока), обозначают j и выражают в ваттах на квадратный метр (Вт/м²):

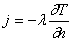(12.4)

Вектор плотности теплового потока направлен по нормали к поверхности в сторону убывания температуры. Векторы j и grad T лежат на одной прямой, но направлены в противоположные стороны.

Тепловой поток q, прошедший сквозь произвольную поверхность S, находят из выражения

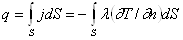(12.5)

Количество теплоты, прошедшее через эту поверхность в течение времени t, определяется интегралом

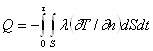(12.6)

Таким образом, для определения количества теплоты, проходящего через какую-либо произвольную поверхность твердого тела, необходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и составляет основную задачу аналитической теории теплопроводности.

В случае стационарного одномерного температурного поля 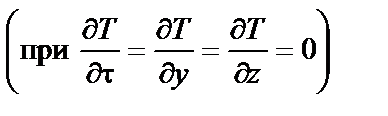закон теплопроводности Фурье имеет наиболее простую запись

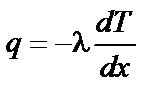(12.7)

Принимая во внимание, что

; ,

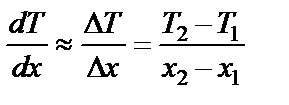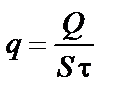закон Фурье (12.7) можно представить в виде:

,

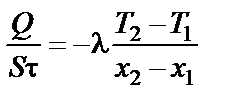т.е. коэффициент теплопроводности l равен количеству тепла Q [дж], протекающему в единицу времени t [с] через изотермическую поверхность площадью S [м²] при перепаде температуры (Т₂ – Т₁) = 1 К на одну единицу длины (х₂ – х₁) = 1 м нормали.

Теплопроводность металлов обусловлена колебаниями кристаллической решетки и движением большого числа свободных электронов (называемых иногда электронным газом). Движение электронов ответственно и за электропроводность металлов, а потому неудивительно, что хорошие проводники тепла (например, серебро или медь) являются также хорошими проводниками электричества. Тепловое и электрическое сопротивление многих веществ резко уменьшается при понижении температуры ниже температуры жидкого гелия (1,8 K). Это явление, называемое сверхпроводимостью, используется для повышения эффективности работы многих устройств – от приборов микроэлектроники до линий электропередачи и больших электромагнитов.