Температурное Поле

Аналитическое исследование теплопроводности сводится к изучению пространственно-временного изменения так называемого температурного поля, характерного для рассматриваемого процесса,

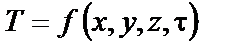, (11.1)

где Т – температура; x, y, z – пространственные координаты в декартовой системе; t – время; f – обозначение функции, определяющей зависимость температуры Т от координат x, y, z и времени t.

Различают стационарное и нестационарное температурное поле.

Выражение (11.1) представляет собой математическую запись нестационарного температурного поля, зависящего не только от пространственных координат x, y, z, но и от времени t.

Стационарным температурным полем называется такое поле,

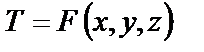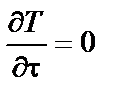, , (11.2)

значение которого в любой его точке не изменяется во времени, т.е. является функцией только пространственных координат x, y, z.

Температурные поля (11.1) и (11.2) являются трехмерными, так как являются функциями трех координат. Если температура есть функция только двух пространственных координат x, y

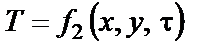; (11.1а)

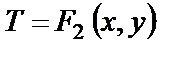, (11.2а)

то температурные поля (11.1а), (11.2а) называют двухмерными. Если же температуры представляют собой функции одной пространственной координаты х

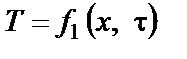; (11.1b)

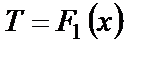, (11.2b)

то соответствующие температурные поля (11.1b), (11.2b) называются одномерными.

Примером одномерных температурных полей могут служить:

- поле неограниченной пластины, ширина и длина которой очень велики по сравнению с ее толщиной;

- поле неограниченного цилиндра, длина которого очень велика по сравнению с его диаметром (радиусом);

- поле шара.

Принимая во внимание, что температура является скалярной величиной, можно утверждать, что температурное поле является скалярным полем.

Если точки поля, имеющие одинаковые температуры, соединить, то получится изотермическая поверхность. Пересечение изотермической поверхности плоскостью дает на этой поверхности изотерму (линию, соответствующую одинаковой температуре).

Вдоль изотермической поверхности температура не изменяется. Наибольшее изменение температуры на единицу длины происходит в направлении нормали n к изотермической поверхности и характеризуется градиентом температуры, представляющим собой вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры

,

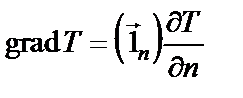где ( 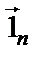) – единичный вектор, направленный по нормали в сторону возрастания температуры; – производная температура по направлению нормали n к изотермической поверхности.

Градиент температуры gradT часто обозначают также символом ÑТ. Составляющие градиента температуры по осям декартовой системы координат равны соответствующим частным производным

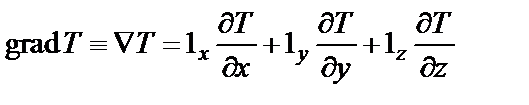, (11.3)

где 1_x, 1_y, 1_z – ортогональные между собой векторы единичной длины, направленные вдоль осей x, y, z соответственно; 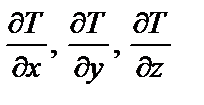– частные производные температуры T (x, y, z, t) по координатам x, y, z.