Теплоотдача при свободном ламинарном движении вдоль вертикальной пластины

Пусть вертикальная пластина с неизменной температурой поверхности, равной t_c, находится в жидкости или газе. Жидкость вдали от пластины неподвижна (вынужденное течение отсутствует), температура жидкости вдали от пластины постоянна и равна t₀. Для простоты вычисления примем, что t_c>t₀ (однако полученные результаты будут справедливы и для обратного соотношения температур). При этом у пластины появляется подъемное движение нагретого слоя жидкости. Вдали от пластины скорость по-прежнему равна нулю. Расположим начало координат у нижней кромки пластины, а ось Оу нормально к ее поверхности (рис. 15.1). Будем полагать, что пластина вдоль оси Oz бесконечна. Процесс стационарный.

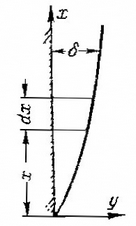
Рис. 15.1. К выводу формулы для коэффициента теплоотдачи при свободной тепловой конвекции

Для упрощения решения задачи примем следующие допущения:

1. силы инерции пренебрежимо малы по сравнению с силами тяжести и вязкости;

2. конвективный перенос теплоты, а также теплопроводность вдоль движущегося слоя жидкости можно не учитывать;

3. градиент давления равен нулю;

4. физические параметры жидкости (исключая плотность) постоянны; плотность является линейной функцией температуры.

Будем полагать, что температура в движущемся слое жидкости изменяется по уравнению

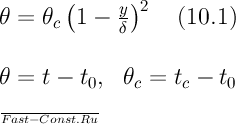15.1

согласно условию задачи θ_c=const. Уравнение (15.1) удовлетворяет граничным условиям (a); коэффициент теплоотдачи определяется уравнением 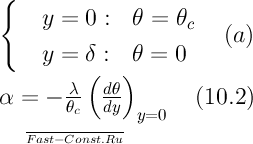(15.2):

15.2

Из уравнения (15.1) следует, что

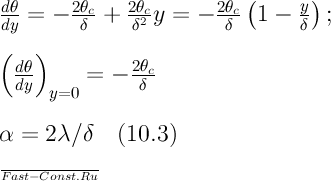
α=2λ/δ (15.3)

Подставляя значение (dθ/dy)_y=0 в уравнение теплоотдачи (15.2), получаем выражение (15.3). Толщина движущегося слоя жидкости переменна по высоте и связана со скоростью движения в этом слое. Поле скоростей описывается уравнением движения. При принятых условиях течение происходит в основном в направлении оси Ох, поэтому используем уравнение движения только в проекциях на ось Ох. Для стационарного течения т с учетом ранее принятых допущений уравнение движения упрощается. В результате будем иметь:

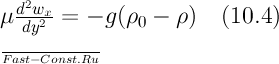15.4

При линейной зависимости плотности от температуры

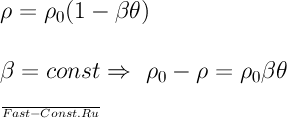
Подставляя значение θ согласно (15.1) в уравнение (15.4) и учитывая последнее соотношение для плотности, уравнение движения можно написать следующим образом:

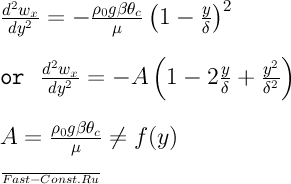
Интегрирование уравнения движения даёт

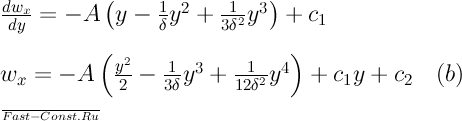
Примем следующие граничные условия для скорости: ω_x=0 как при у=0, так и при у=δ. Отметим, что, строго говоря, при y=δ (θ=0) скорость может быть не равна нулю. Это объясняется действием сил вязкости. Движущиеся частицы могут увлекать за собой слои жидкости, находящиеся в изотермических условиях. При принятых граничных условиях из уравнения (b) следует, что

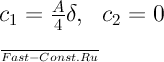
Подставив значения c₁ и с₂ в уравнение (b) и произведя некоторые преобразования, получим следующее уравнение распределения скоростей в движущемся слое жидкости:

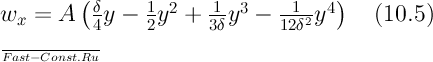
На рис. 15.2 приведено распределение скоростей согласно уравнению (15.5). Здесь же представлена кривая температур согласно уравнению (15.1).

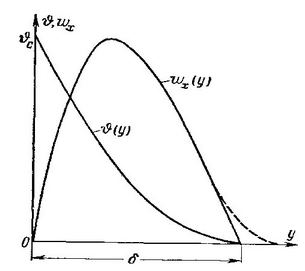
Рис. 15.2. Распределение температуры и скорости согласно уравнениям (15.1) и (15.5)

Максимум скорости соответствует значению:

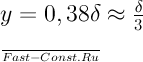
Заметим, что распределение скоростей при y=δ не удовлетворяет условию (dω_x/dy)_y=δ=0. Производная при у=δ имеет конечное значение. Это обстоятельство является следствием приближенности решения. Характер изменения скорости на внешней границе движущегося слоя показан пунктирной линией. Согласно уравнению (15.5) среднеинтегральная скорость равна:

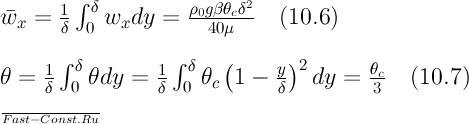(15.7)

Для простоты решения среднюю температуру жидкости в слое определим приближенно как среднеинтегральную по сечению слоя дает:

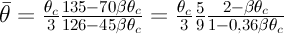
что при малых θ_с незначительно отличается от θ_с/3) и получим выражение (15.7). Таким образом, при принятых условиях величина средней температуры слоя не зависит от координаты x. Расход жидкости через поперечное сечение слоя 6·1 равен:

G= ρ₀ 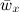δ (15.8)

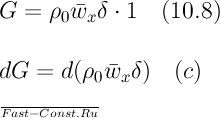
Расход жидкости определен по плотности ρ₀. При этом полагаем, что жидкость плотностью ρ₀, вовлекаясь в движущийся слой, приобретает в среднем скорость 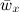. Подставляя в (c) значение 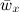согласно уравнению (15.6), получаем:

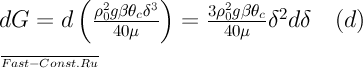
В движение вовлекается жидкость с первоначальной температурой t₀. В движущемся слое эта жидкость нагревается до различных температур, лежащих в интервале от t₀ до t_c. Можно считать, что в среднем жидкость нагревается до температуры 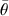. На этот нагрев затрачивается теплота

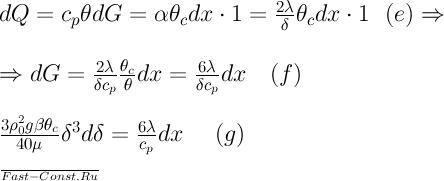
Приравнивая правые части уравнений (d) и (f), получаем дифференциальное уравнение, описывающее изменение δ по высоте стенки - выражение (g). Интегрируя это уравнение получаем:

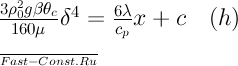
Постоянную интегрирования с найдем из условия, что при х=0 δ=0. Отсюда с=0. Из уравнения (h) следует, что

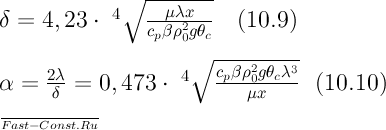(15.10)

Согласно уравнению (15.3) 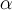=2λ/δ. Подставляя сюда значение δ, получаем выражение (15.10).

Приведем уравнение (15.10) к безразмерному виду, для чего левую и правую части уравнения умножим на х и разделим на λ. После некоторых преобразований получим

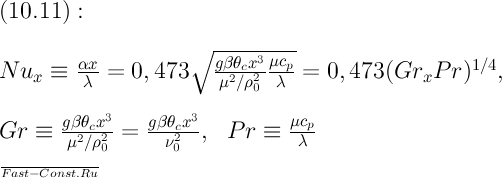(15.11)

Как следует из уравнения (15.11), Nu_x=ƒ(Gr_xPr). Такой же результат дает теория подобия. Произведение чисел Gr и Рr часто называют числом Рэлея и обозначают символом Ra. В рассматриваемом случае температуры t_c и t₀ постоянны, следовательно, неизменен и температурный напор θ_c=t_c—t₀. При этом осреднение коэффициента теплоотдачи дает один и тот же результат. Из уравнения (15.11) следует, что 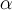=сх^–0,25, где c≠ƒ(х). При этом

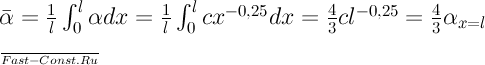
где 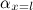- местный коэффициент теплоотдачи в точке, определяемой координатой х= 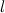. Тогда средняя теплоотдача вертикальной пластины при t_c=const в ламинарном течении

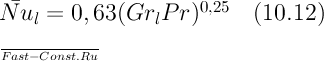
Коэффициенты пропорциональности в формулах (15.11) и (15.12) нуждаются в некоторых уточнениях. Формулы (15.11) и (15.12) получены при ряде упрощающих допущений. В частности, при выводе этих формул не учитывались силы инерции. Расчеты, проведенные с учетом сил инерции, показывают, что коэффициент пропорциональности в формулах (15.11) или (15.12) зависит от числа Прандтля. Результаты точных решений, выполненных Польгаузеном, Шу, Саундерсом, Греггом и Спэрроу, приведены на графике рис. 15.3.

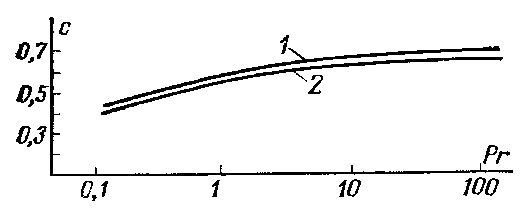
Рис. 15.3. Зависимость теплоотдачи при свободной конвекции от числа Прандтля 1 — q_c=const, 2 — t_c=const

Здесь c=Nu_x(Gr_xPr)^–0,25. Наиболее существенно проявляется влияние инерционных сил при небольших значениях чисел Прандтля. Кроме того, из рис. 15.3 следует, что интенсивность теплоотдачи при постоянной температуре стенки примерно на 7% меньше, чем при постоянной плотности теплового потока на стенке. Экспериментальные исследования показывают, что при числах Прапдтля, больших примерно 0,7, опытные данные можно описать формулой вида (15.11) или (15.12) с постоянными коэффициентами, однако значение коэффициентов несколько иное, чем в полученных ранее формулах. Помимо других причин, величина коэффициентов пропорциональности зависит от выбора определяющей температуры. Для расчета местных коэффициентов теплоотдачи при свободном ламинарном течении вдоль вертикальных стенок можно использовать формулу:

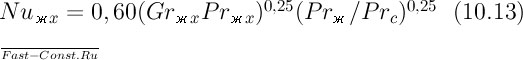(15.13)

Здесь определяющей является температура жидкости за пределами движущегося слоя (Рr_c выбирается по местной температуре стенки). Определяющий размер (продольная вдоль потока координата) отсчитывается от места начала теплообмена. На рис. 15.4 формула (15.13) сопоставлена с опытными данными.

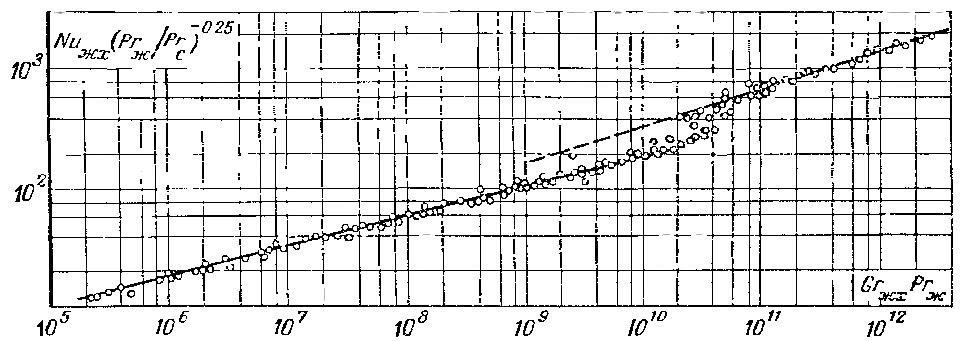
Рис. 15.4. Теплоотдача при свободной конвекции у вертикальной поверхности в большом объеме жидкости

Формула (15.13) получена при условии, что q_c=const. Осредняя коэффициенты теплоотдачи, получаем, что при q_c=const:

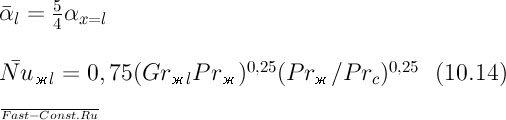(15.14)

Здесь определяющей температурой по-прежнему является температура жидкости за пределами движущегося слоя, определяющий размер — длина пластины, отсчитываемая от начала теплообмена.

Формула (15.13) получена для теплоносителей с числами Прандтля от 0,7 до 3×10³. Ею следует пользоваться при 10³<Gr_жxРr_ж<10⁹. Уравнение (15.13) получено при условии q_c=const. Исходя из графика рис. 15.3, для случая t_c=const значение коэффициента пропорциональности в формуле (15.13) в первом приближении может быть взято равным примерно 0,55. При этом

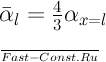
Вертикальная труба и пластина: ламинарное течение - 10³<(Gr ·Pr)_ж <10⁹:

Nu_жdср. = 0,75· (Gr_жd ·Pr _ж)^0,25·(Pr _ж/Pr_ст)^0,25 .

Здесь значения Gr_жd и Pr _ж берутся при температуре жидкости (газа), а Pr_ст при температуре поверхности стенки. Для воздуха Pr _ж/Pr_ст = 1.