ТЕРМОДИНАМИКА ГАЗОВОГО ПОТОКА
4.1. Уравнения и параметры движущегося газа
В рассмотренных выше процессах не учитывалась кинетическая энергия рабочего тела. Однако в теплотехнике широко распространены энергетические установки, в которых преобразование энергии осуществляется в движущемся газе. Такие процессы происходят в турбинах, реактивных двигателях, лопаточных и струйных компрессорах и т.п.
Рассмотрим уравнения термодинамики для стационарного одномерного потока идеального газа.
Для газового потока в любом сечении справедливо уравнение состояния, записанное через плотность:
p = ρRT, (4.1)
где p – давление в рассматриваемом сечении;
ρ – плотность газа в этом сечении;
R – газовая постоянная;
T – термодинамическая температура (температура, которую покажет в данном сечении безинерционный термометр, перемещающийся со скоро-стью газового потока).
В термодинамике величину скорости потока газа обозначают с и измеряют в м/с. Часто с целью количественной оценки величины скорости потока ее сравнивают со скоростью распространения слабых возмущений в среде газа. При выведении газа из равновесия в каком-либо месте в нем возникает движение частиц. Эти возмущения передаются по всему газу (подвижному и неподвижному) с так называемой с к о р о с т ь ю з в у к а. Скорость звука обозначается a, измеряется в м/с и вычисляется поизвестной из физики формуле:
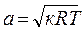 . (4.2)
. (4.2)
Если c < 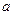 , то поток дозвуковой, при c>
, то поток дозвуковой, при c> 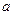 – сверхзвуковой.
– сверхзвуковой.
4.1.1. Уравнение энергии
В движущемся газе выделим сечениями 1-1 и 2-2, Рис. 4.1, участок потока.

Рис.4.1
На основании первого закона термодинамики для энергоизолирован- ного потока (данная система не обменивается теплотой и работой с окружающей средой) можем записать Е1 = Е2. Отсюда для m = 1кг газа уравнение (1.7) в сечениях потока будет иметь вид:
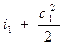 =
= 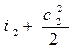 .
.
Это означает, что для любого сечения потока газа сумма энтальпии и кинетической энергии одинакова, т.е.
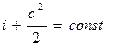 . (4.3)
. (4.3)
Выражение (4.3) называют у р а в н е н и е м э н е р г и и потока газа. Из него следует, что изменить скорость газа в потоке можно лишь только за счет изменения энтальпии.
Уравнение энергии можно записать в другом виде. Продифференцируем выражение (4.3) и получим: cdc = - di. Из первого закона термодинамики, записанного в виде dq = di -vdp, при dq = 0 следует, что di = vdp. Тогда
c dc = - v dp. (4.4)
Выражение (4.4) приписывают Д. Бернулли, поэтому в технической литературе его называют у р а в н е н и е м Б е р н у л л и.
Это уравнение устанавливает связь скорости с давлением. Из него следует, что для увеличения скорости (dc > 0) необходимо снижение давления (dp < 0) и наоборот.
4.1.2. Параметры торможения
Если на пути движущегося газа поставить преграду, то в сечении, где поток полностью затормозится (c = 0), параметры газа называют п а р а -
м е т р а м и т о р м о ж е н и я. Их обозначают p0 , T0 , ρ0 . Для замкнутого объема с неподвижным газом, параметры газа соответствуют параметрам торможения.
Определим параметры торможения движущегося газа. Для этого запишем уравнение энергии для двух сечений: в одном газ движется со скоростью c, а в другом – поток заторможен:
i + 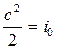 .
.
Выразим энтальпию газа через теплоемкость и температуру:
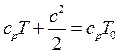 .
.
Из этого выражения определим температуру торможения:
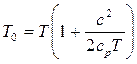 ,
,
Так как 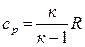 и
и 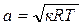 , то:
, то:
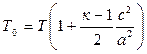 ,
,
где 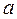 – "местная" скорость звука (в сечении с температурой T).
– "местная" скорость звука (в сечении с температурой T).
Отношение 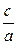 обозначают через Ма и именуют числом Маха.
обозначают через Ма и именуют числом Маха.
В окончательном виде формула температуры торможения имеет вид:
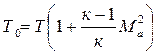 . (4.5)
. (4.5)
Используя адиабатную связь между температурой и давлением, получим формулу для давления торможения:
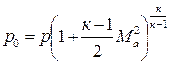 . (4.6)
. (4.6)
Плотность ρ0 определяется по p0 и T0 из уравнения (4.1).
4.1.3. Уравнение скорости движения газа
Уравнение скорости движения газа в произвольном сечении потока получим из уравнения энергии. Пусть газ вытекает из емкости, где его скорость была равна нулю. Тогда уравнение энергии для произвольного сечения потока газа и для сечения, где c = 0, будет иметь вид:
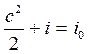 .
.
Отсюда
c = 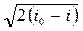 =
= 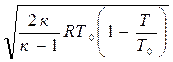 .
.
Если отношение температур заменить отношением давлений, то
c= 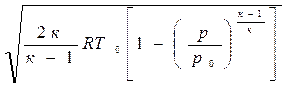 . (4.7)
. (4.7)
Из выражения (4.7) следует, что величина скорости газа в рассматриваемом сечении потока зависит от природы газа, от параметров в его исходном (заторможенном) состоянии и от давления газа в рассматриваемом сечении.
4.1.4. Уравнение расхода
Термодинамика газового потока в основном рассматривает стационарное движение газа. Это означает, что через все сечения канала в любой момент времени протекает одно и то же массовое количество газа. Обозначается секундный массовый расход 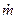 , который измеряется в кг/с. Уравнение для вычисления секундного массового расхода выводится в дисциплине “Газовая динамика”. Оно имеет вид:
, который измеряется в кг/с. Уравнение для вычисления секундного массового расхода выводится в дисциплине “Газовая динамика”. Оно имеет вид:
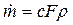 . (4.8)
. (4.8)
Выразим секундный массовый расход через параметры заторможенного газового потока, для чего в выражение (4.8) вместо c подставим его значение (4.7), а плотность представим в виде
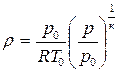 .
.
Тогда
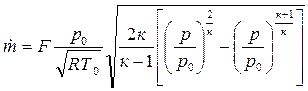 (4.9)
(4.9)
4.2. Течение газа в каналах
4.2.1. Уравнение обращения воздействия
Каналы, в которых газовый поток увеличивает свою скорость, называются с о п л а м и. Каналы, скорость в которых уменьшается, именуют д и ф -ф у з о р а м и. Геометрическая форма сопел может быть различной. Это зависит от того, каково внешнее воздействие на газовый поток.
В 1948 г. А.А. Вулис получил зависимость, выражающую связь геометрии сопла с характером внешнего воздействия на поток. Для неэнергоизолированного движения газа зависимость Вулиса имеет вид:
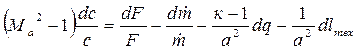 . (4.10)
. (4.10)
Здесь первое слагаемое правой части уравнения выражает г е о м е т-
р и ч е с к о е в о з д е й с т в и е на движущийся газ, второе – м а с с о в о е, третье – т е п л о в о е и четвертое – м е х а н и ч е с к о е. Уравнение (4.10) является математическим выражением принципа обращения воздействия, суть которого состоит в том, что характер влияния каждого воздействия на газовый поток противоположен при сверхзвуковых и дозвуковых течениях газа.
Проанализируем лишь геометрическое воздействие. В этом случае из уравнения (4.10) следует:
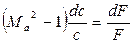 . (4.11)
. (4.11)
При дозвуковом течении газа (Мa < 1) знаки у величин dc/c и dF/F
противоположны. Это значит, что в сужающемся канале, где dF < 0, газ будет разгоняться, т.е. dc > 0, а в расширяющемся, где dF > 0, – тормозиться, т.е. dc< 0.
При сверхзвуковом потоке газа (M >1) знаки у величин dc/c и dF/F одинаковые. Следовательно, для увеличения скорости необходим расширяющий канал, а для торможения - сужающийся.
 Таким образом, канал для разгона газового потока до сверхзвуковой скорости должен быть сужающе-расширяющимся и иметь вид, представленный на рис. 4.2. Впервые канал такой формы предложил шведский инженер Лаваль, в его честь такие каналы именуют соплами Лаваля.
Таким образом, канал для разгона газового потока до сверхзвуковой скорости должен быть сужающе-расширяющимся и иметь вид, представленный на рис. 4.2. Впервые канал такой формы предложил шведский инженер Лаваль, в его честь такие каналы именуют соплами Лаваля.
Рис. 4.2
4.2.2 Течение газа в соплах Лаваля
При движении газа вдоль сверхзвукового геометрического сопла своеобразно изменяются его параметры. Для выявления характера изменения давления по длине сопла из уравнений (4.4) и (4.11) можно получит выражение:
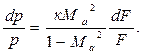
Из анализа данного уравнения следует, что давление вдоль сопла уменьшается. Кривая давления в дозвуковой части сопла имеет выпуклый вид, а в сверхзвуковой – вогнутый. Температура вдоль сопла уменьшается, так как процесс расширения газа адиабатный. С такой же закономерностью уменьшается по длине сопла и скорость звука.
Характер изменения скорости вдоль сопла устанавливается уравнением Бернулли (4.4), записанным в виде:
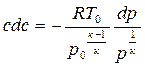 .
.
В сужающейся части сопла это вогнутая кривая. а в расширяющейся – выпуклая, асимптотически приближающаяся к максимально возможной скорости при р = 0. Качественные изменения давления, температуры, скорости звука и скорости потока по длине геометрического сопла представлены на рис.4.3 .Характерным для канала такой формы является участок перехода дозвукового течения в сверхзвуковой.
Сечение канала, в котором скорость потока достигает величины, равной местной скорости звука, называют к р и т и ч е с к и м .
 Параметры газа в критическом сечении обозначают: скр, ркр, Ткр, ρкр,
Параметры газа в критическом сечении обозначают: скр, ркр, Ткр, ρкр, 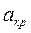 , и т.д.
, и т.д.
Получим выражение для ркр и Ткр через параметры торможения. В критическом сечении 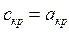 , следовательно:
, следовательно:
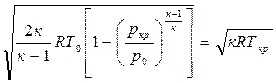
После незначительных преобра –
зований получим:
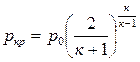 . (4.12)
. (4.12)
Если обозначить:
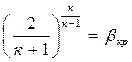 ,
,
то
ркр = р0 βкр .
Величина β определяется только
значением показателя адиабаты к . Рис. 4.3
Так, для воздуха при к = 1,4 значение βкр = 0,528. Отсюда следует, что для воздуха критическое давление меньше давления торможения в 1,89 раза.
Значение критической температуры получим из выражения (4.12), заменив отношение давлений отношением температур:
Ткр= Т0 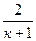 (4.13)
(4.13)
Теперь выражение для критической скорости можно представить в другом виде:
скр = 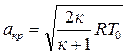 . (4.14)
. (4.14)
Скорость газа в каждом сечении сопла и на выходе из него вычисляется по формуле (4.7).
Если секундный массовый расход выразить через параметры торможения и площадь критического сечения, то зависимость (4.9) существенно упрощается:
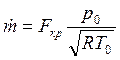
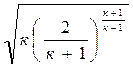 . (4.15)
. (4.15)
.
Если давление газа в выходном сечении сопла равно давлению окружающей среды ( 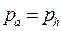 ), то сопло работает на расчетном режиме; при pa >ph газ на выходе из сопла недорасширяется. Возможны режимы работы сопел, когда давление на выходе в потоке незначительно меньше давления окружающей среды (pa<ph ), в этом случае происходит перерасширение газа.
), то сопло работает на расчетном режиме; при pa >ph газ на выходе из сопла недорасширяется. Возможны режимы работы сопел, когда давление на выходе в потоке незначительно меньше давления окружающей среды (pa<ph ), в этом случае происходит перерасширение газа.
4.2.3. Дросселирование газа и пара
Д р о с с е л и р о в а н и е м называют процесс понижения давления в газовом потоке при преодолении местного сопротивления в канале.
При дросселировании газа или пара протекает необратимый процесс снижения давления без совершения внешней работы. Если в канале имеется местное сопротивление в виде резкого сужения вида перегородки с отверстием, задвижки, клапана и т.п., то газовый поток перестраивает свою геометрическую форму, как до сужения, так и после него. Перестройка формы потока и перетекание через само сужение связано с образованием вихревых движений газа. Часть кинетической энергии потока идет на образование вихрей, часть – на преодоление сопротивления трения. Затраченная на это энергия необратимо превращается в теплоту, которая воспринимается газом. Поэтому давление после местного сопротивления не восстанавливается до первоначального. Изменение давления, скорости и температуры по длине канала приведено на рис.4.4. Скорость газа при протекании его через сужение возрастает, что вызывает снижение давления и температуры. После сужения скорость понижается, но давление, вследствие указанных причин, не восстанавливается до первоначального.
Степень снижения давления газа при дросселировании зависит от природы газа и его состояния, относительной величины сужения, скорости газа. Обозначим степень снижения давления через 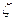 ; тогда ее величина будет равна:
; тогда ее величина будет равна:

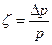 ,
,
где ∆р – величина снижения давления;
р – давление на входе в сужение.
В энергетических установках дросселирование нежелательно, т.к. при падении давления снижаются энергетические возможности газа. Но иногда дросселирование является необходимым и создается искусственно, например, в редукторах, регуляторах и т.п.
При термодинамическом анализе особенностей процесса дросселирования целесообразно использовать общее уравнение энергии:
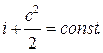
В канале можно обеспечить с1 = с2 , тогда i1 =i2. Из чего следует, что энта-
льпия газа в процессе дросселирования
остается постоянной. Рис. 4.4
Этот вывод справедлив как для идеальных, так и для реальных газов. При дросселирования идеального газа Т1 = Т2 , поскольку i1 = i2 . Это значит, что для идеального газа температура после дросселирования равна температуре на входе в дроссель.
Для реального газа изменение температуры при его дросселировании в отличие от идеального газа имеет своеобразный характер. Как показывают опыты, температура реального газа в результате дросселирования повышается, понижается или не изменяется. Это свойство впервые обнаружили ученые Д. Джоуль и У. Томсон, поэтому оно носит название э ф ф е к т а Д ж о у л я-Т о м с о н а.
Используя дифференциальные уравнения, связывающие i, s, ρ и T, можно получить для газа, подчиняющегося уравнению Ван-дер-Ваальса, следующую зависимость:
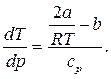 (4.16)
(4.16)
Отношение бесконечно малого изменения температуры к бесконечно малому изменению давления при дросселировании называется д р о с с е л ь-э ф ф е к т о м и обозначается
α = 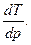
Так как при дросселировании dp < 0, а cp – величина положительная, то знак α будет зависеть от знака числителя выражения (4.16).
При этом возможны три случая:
а) 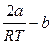 < 0 ( при T <
< 0 ( при T < 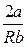 ), тогда α > 0, т.е. dT < 0;
), тогда α > 0, т.е. dT < 0;
б) 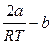 > 0 ( при T >
> 0 ( при T > 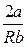 ), тогда α < 0, т.е. dT > 0;
), тогда α < 0, т.е. dT > 0;
в) 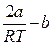 = 0 ( при T =
= 0 ( при T = 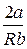 ), тогда α = 0, т.е. dT = 0.
), тогда α = 0, т.е. dT = 0.
Изменение знака дроссель - эффекта α называется и н в е р с и е й,
а температура, при которой dT = 0, называется т е м п е р а т у о й и н в е р с и и и обозначается Tинв .
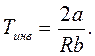 (4.17)
(4.17)
|
Каждый конкретный газ имеет индивидуальную температуру инверсии. Так, например, для воздуха Тинв = 650 К; для водорода Тинв = 204 К; для водяного пара Тинв= 682 К.
Для установления температуры реального газа после дросселя необходимо сравнить Tвх с Tинв .Если температура газа на входе в дроссель равна его температуре инверсии, то после дросселя она восстановится до прежнего значения. При Tвх< Tинв температура газа после дросселя уменьшится, а . при Tвх> Tинв - она возрастет. Характер изменения температуры при дросселировании
 Глава 5
Глава 5
Дата добавления: 2015-02-16; просмотров: 6592;
