Относительная влажность
Отношение действительного значения абсолютной влажности к максимально возможному ее значению при той же температуре называется о т н о с и т е л ь н о й влажностью.
Обозначают относительную влажность φ :
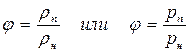 (3.3)
(3.3)
Как правило, относительную влажность выражают в процентах, тогда
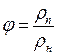 ∙ 100, % и
∙ 100, % и 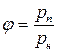 ∙ 100, %.
∙ 100, %.
Для сухого воздуха φ = 0%, влажный насыщенный воздух имеет φ = 100%.
Увеличение относительной влажности воздуха происходит за счет добавления в него количества водяного пара. В тоже время, если охлаждать влажный воздух при неизменном парциальном давлении водяного пара, то φ будет увеличиваться вплоть до φ = 100%.
Температуру, при которой достигается состояние насыщения влаж- ного воздуха, называют т е м п е р а т у р о й т о ч к и р о с ы и обозначают tр .
При температуре ниже tр воздух будет оставаться насыщенным, избыточная же влага выпадает из влажного воздуха в виде капель воды или тумана. Это свойство положено в основу принципа определения tр прибором, называемым гигрометром.
При обработке влажного воздуха (подогрев, охлаждение) количество сухого воздуха в нем не изменяется, поэтому целесообразно все удельные величины относить к 1 кг сухого воздуха.
Массу водяного пара, приходящуюся на 1 кг сухого воздуха, называютют в л а г о с о д е р ж а н и е м.
Обозначают влагосодержание через d, измеряют в г/кг.
Из определения следует:
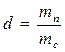 . (3.4)
. (3.4)
При допущении, что водяной пар и сухой воздух являются идеальными газами, можно записать:
pп Vп = mпRпТп и pс Vc = mcRcTс .
Почленно разделим их и, учитывая особенности газовых смесей (пар и сухой воздух занимают один и тот же объем и имеют одинаковую температуру), т.е. Vп = Vc и Tп = Тс), получим:
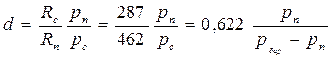 (3.5)
(3.5)
Из уравнения (3.5) следует, что влагосодержание при заданном барометрическом давлении (рбар) зависит только от парциального давления водяного пара. В выражение (3.5) можно ввести значение относительной влажности φ: так, с учетом (3.3)
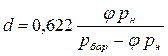 . (3.6)
. (3.6)
Из уравнения (3.5) определим парциальное давление водяного пара во влажном воздухе через влагосодержание:
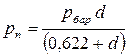 . (3.7)
. (3.7)
3.2.2. Диаграмма id влажного воздуха
Определение параметров влажного воздуха и расчет процессов тепло- и массообмена значительно упрощается при использовании id – диаграммы, которая была предложена в 1918 г Л.К.Рамзиным. Диаграмма (рис. 3.3) построена для барометрического давления 745 мм рт. ст., т.е. 99,3 кПа (среднее годовое давление в Центральной части России), но ею можно пользоваться и при других барометрических давлениях в пределах допустимой точности.
При построении диаграммы по оси ординат отложена удельная энтальпия сухого воздуха – i, а по оси абсцисс влагосодержании – d. С целью расширения наиболее используемой для расчетов области, соответствующей насыщенному влажному воздуху, угол между осями выбран равным 1350. Горизонтально проведена вспомогательная ось, на которую спроецированы значения влагосодержания с наклонной оси. Хотя ось абсцисс на диаграмму обычно не наносится, изоэнтальпы идут параллельно ей, поэтому они на диаграмме изображаются наклонными прямыми. Линии d = const проведены параллельно оси ординат.
Значения d = const и i = const образуют координатную сетку, на которую наносятся линии постоянных температур (изотермы) и кривые линии относительной влажности (φ=const).
Для построения изотерм необходимо выразить энтальпию через влагосодержание. Энтальпия влажного воздуха на основании условия аддитивности выразится как
I = Ic + Iп .
Поделим величины данного уравнения на массу сухого воздуха, получим:
i = ic + 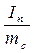 .
.
Если второе слагаемое умножить и разделить на массу пара, то будем иметь:
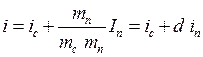 (3.8)
(3.8)
Отсчитывая энтальпию от 00С, выражение (3.8) можно записать:
i = cpct + d (r0 + cpп t), (3.9)
где cpc и cpп – массовые теплоемкости сухого воздуха и пара;
r0 – теплота фазового перехода воды в пар при 00С;
t – текущее значение температуры.
При допущении, что теплоемкости сухого воздуха и пара в диапазоне измеряемых температур постоянны, для фиксированного t уравнение (3.9) представляет линейную зависимость i от d. Следовательно, изотермы в координатах i d будут прямыми линиями.
Используя выражение (3.6) и табличные зависимости давления насыщенного пара от температуры pн = f(t), несложно построить кривые относительной влажности. Так, при построении кривой для конкретного φ выбирают несколько значений температур, из таблиц для них определяют pн и по (3.6) вычисляют d. Соединив точки с координатами ti,, di линией, получим кривую φ = const. Линии (φ = const) имеют вид расходящихся кривых, которые претерпевают излом при t = 99,4 0С (температура кипения воды при давлении 745 мм рт. ст), и дальше идут вертикально. Кривая φ=100% делит площадь диаграммы на две части. Выше кривой располагается область влажного воздуха с ненасыщенным паром, а ниже – область влажного воздуха с насыщенным и частично – с конденсированным паром. Изотермы, соответствующие температурам адиабатного насыщения воздуха (tм), на диаграмме проходят под небольшим углом к изоэнтальпам и изображены пунктирными линиями. Они измеряются "мокрым" термометром и обозначаются tм. На кривой φ = 100 % в одной точке пересекаются изотермы сухого и мокрого термометров. В нижней части диаграммы по уравнению (3.7) построена зависимость рп= f(d) для рбар = 745 мм рт ст.
По id-диаграмме, зная два любых параметра, можно определит все остальные параметры влажного воздуха. Так, например, для состояния A
(см рис. 3.6) имеем ta, ia, φa, da, pпа, tp. Значения температуры ta, энтальпии ia и влагосодержания da есть проекция точки А на оси i, d и t. Величина относительной влажности характеризуется значением на кривой, проходящей через данное состояние.
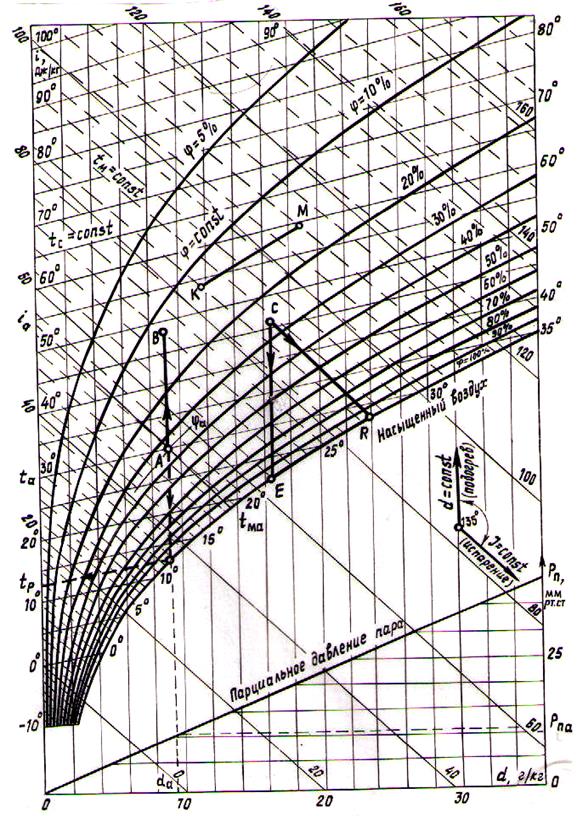
Рис. 3.3
Для определения температуры точки росы необходимо точку A спроецировать на кривую φ = 100%. Изотерма, проходящая через эту проекцию, дает значение tp. Давление пара определяется по влагосодержанию da и линией pп = f(d).
При нагревании воздуха его влагосодержание не изменяется (d=const), а энтальпия возрастает, поэтому процесс нагрева на id-диаграмме изображается вертикальной прямой AB.
Процесс охлаждения воздуха также происходит при d=const; энтальпия уменьшается (линия CE), а относительная влажность возрастает вплоть до точки росы, являющейся пересечением прямой охлаждения CE с кривой φ = 100 %.
В процессе сушки материала воздух увлажняется. Если при этом теплота, истраченная на испарение влаги, берется из воздуха, то этот процесс приближенно (без учета энтальпии воды) считают изоэнтальпным, так как израсходованная теплота снова возвращается воздуху вместе с испаренной влагой. Поэтому на id – диаграмме процесс сушки изображается прямой CR, параллельной линиям i = const.
При увлажнении воздуха паром (линия КМ) энтальпия влажного воздуха увеличивается. Параметры состояния (iм , dм) определяются по начальным (iк, dк),. из теплового и материального балансов процесса смешения
iм = iк + dп iп и dм = dк + dп ,
где iп и dп – энтальпия и количество подаваемого пара на 1 кг сухого воздуха, соответственно.
При смешивании потоков влажного воздуха параметры смеси определяются на основании балансов массы, энтальпии и влаги. Если расходы влажного воздуха в смешиваемых потоках 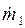 и
и 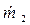 , а энтальпии и влагосодержания, соответственно, i1, d1 и i2, d2, то уравнения для определения энтальпии и влагосодержания смеси следующие:
, а энтальпии и влагосодержания, соответственно, i1, d1 и i2, d2, то уравнения для определения энтальпии и влагосодержания смеси следующие:
iсм = (i1m1 + i2m2)/(m1+m2) ,
dсм = (d1m1+d2m2)/(m1+m2).
При смешении двух потоков воздуха относительная влажность смеси не может быть больше 100 %.
Дата добавления: 2015-02-16; просмотров: 2445;
