Диаграмма Вышнеградского
Влияние распределения корней на характер переходного процесса и на устойчивость хорошо иллюстрирует диаграмма, построенная И.А. Вышнеградским для нормированного характеристического уравнения третьего порядка
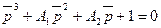 .
.
 Область устойчивости в плоскости параметров А1 и А2 состоит из трех областей, соответствующих различному распределению корней. Область I, ограниченная линией abc, соответствует трем действительным (и не равным друг другу) корням и апериодическому переходному процессу. Область II, ограниченная линией abd, соответствует паре комплексных корней и одному действительному корню, причем действительный корень ближе к мнимой оси, чем комплексные. Переходный процесс в этом случае монотонный. В области III, заключенной между границей устойчивости и линией abc, также пара комплексных корней и один действительный, но к мнимой оси ближе расположены комплексные корни. Переходный процесс колебательный.
Область устойчивости в плоскости параметров А1 и А2 состоит из трех областей, соответствующих различному распределению корней. Область I, ограниченная линией abc, соответствует трем действительным (и не равным друг другу) корням и апериодическому переходному процессу. Область II, ограниченная линией abd, соответствует паре комплексных корней и одному действительному корню, причем действительный корень ближе к мнимой оси, чем комплексные. Переходный процесс в этом случае монотонный. В области III, заключенной между границей устойчивости и линией abc, также пара комплексных корней и один действительный, но к мнимой оси ближе расположены комплексные корни. Переходный процесс колебательный.
На диаграмме показано также распределение корней для разграничительных линий. В точке b, в которой А1=А2=3, все три корня действительные и равные друг другу.
Частотные методы базируются на прямом и обратном преобразовании Фурье.
Если f(t) – функция периодическая, то для нее применимо:

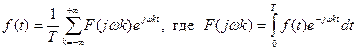
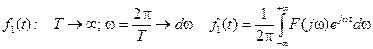
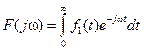
Будем рассматривать: 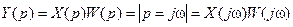
Y(t)=h(t); x(t)=1(t) 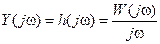
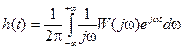
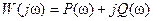 ,
, 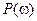 - вещественная характеристика.
- вещественная характеристика.
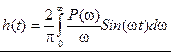
Дата добавления: 2015-02-16; просмотров: 1117;
