Влияние полюсов передаточной функции на качество переходных процессов
Каждому полюсу li на комплексной плоскости соответствует определенная точка. Данные корни определяют на плоскости следующую замкнутую плоскость.
В корневых методах используют так называемые корневые показатели, определяемые по расположению корней
р1, р2, …, рп характеристического уравнения замкнутой системы на комплексной плоскости.
1) Наиболее общим корневым показателем качества является среднее геометрическое значение модулей корней
,
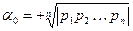которое легко вычисляется через крайние коэффициенты характеристического уравнения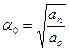 
. a0 определяет центр расположения всех корней характеристического уравнения и влияет на быстродействие системы. Чем меньше показатель a0, тем ближе «созвездие» корней к мнимой оси и тем больше длительность переходного процесса.
Пусть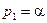 
: Чем ближе 
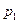к мнимой оси, тем ближе САУ к границе устойчивости. Поскольку 
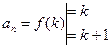- где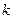 
- передаточный коэффициент разомкнутого контура для астатических систем, а 
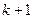- для статических систем.
| |
2) Расстояние от мнимой оси до действительной части ближайшего к ней корня называется степенью устойчивости h.
3) Колебательные свойства системы регулирования предопределяет k–ая пара комплексных корней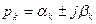 
, для которой наибольшее отношение
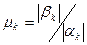
или наибольший угол j между действительной осью и лучами, соединяющими начало координат с этими корнями. В данном случае такой парой являются комплексные корни р2 и р3.
Отношение mд мнимой части b к действительной части a доминирующей пары комплексных корней называют степенью колебательности.
В практических расчетах чаще используют корневой показатель колебательности
,
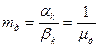также определяемый через доминирующую пару комплексных корней. При выборе настроек регуляторов стремятся получить значения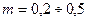 
.
4) Абсолютное значение x действительной части корня, наиболее удаленного от мнимой оси.
Дата добавления: 2015-02-16; просмотров: 1079;