Действие магнитного поля на движущуюся заряженную частицу
Мы уже знаем, что на проводник с током, помещенный в магнитное поле, действует сила Ампера. Но ток в проводнике – есть направленное движение зарядов. Отсюда напрашивается вывод, что сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, от которых это действие передается уже самому проводнику.
Сила Ампера, действующая на элемент тока в магнитном поле с индукцией  :
:
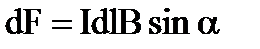 ,
,
где α – угол между направлением тока в проводнике и вектором  .
.
Пусть  – скорость упорядоченного движения зарядов в проводнике; q– заряд носителя тока (в металлах q = - e). Для элемента тока можем написать:
– скорость упорядоченного движения зарядов в проводнике; q– заряд носителя тока (в металлах q = - e). Для элемента тока можем написать:
 dNq
dNq  ,
,
где n = dN/dV – концентрация зарядов, dN – число зарядов в элементе объема dV = Sdl.
Тогда, сила, действующая в магнитном поле на один заряд, будет:

Сила, действующая на электрический заряд q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой

где В — индукция магнитного поля, в котором заряд движется.
Направление силы Лоренца определяется с помощью правила левой руки:если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для q > 0направления
| Рисунок 2.1 - Направление силы Лоренца |

|

|
| б) q < 0 |
|

|
 
|
| a) q > 0 |

|
На рис. 2.1 показана взаимная ориентация векторов v, В и F для положительного и отрицательного зарядов.
На отрицательный заряд сила действует в противоположном направлении. Модуль силы Лоренца равен

где a — угол между v и В.
Отметим еще раз, что магнитное поле не действует на покоящийся электрический заряд.В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды.
Так как по действию силы Лоренца можно найти модуль и направление вектора В, то выражение для силы Лоренца может быть использовано для определения вектора магнитной индукции В.
Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
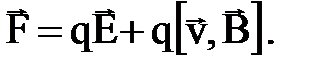
Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы,действующей со стороны электрического поля, и силы Лоренца:
Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.
Дата добавления: 2015-02-13; просмотров: 1643;
