Основные формулы. где - магнитная индукция поля, создаваемого элементом проводника с током; μ – магнитная проницаемость; - магнитная постоянная ( Гн/м); - вектор
Закон Био-Савара-Лапласа
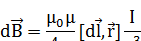
где 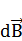 - магнитная индукция поля, создаваемого элементом проводника с током; μ – магнитная проницаемость;
- магнитная индукция поля, создаваемого элементом проводника с током; μ – магнитная проницаемость; 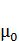 - магнитная постоянная (
- магнитная постоянная ( 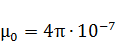 Гн/м);
Гн/м); 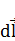 - вектор, равный по модулю длине dl проводника и совпадающий по направлению с током (элемент проводника); I – сила тока;
- вектор, равный по модулю длине dl проводника и совпадающий по направлению с током (элемент проводника); I – сила тока;
 – радиус-вектор , проведенный от середины элемента проводника к точке, в которой определяется магнитная индукция.
– радиус-вектор , проведенный от середины элемента проводника к точке, в которой определяется магнитная индукция.
Модуль вектора 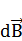 выражается формулой
выражается формулой
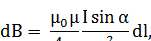
где α – угол между векторами 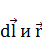 .
.
Магнитная индукция 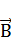 связана с напряженностью
связана с напряженностью 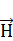 магнитного поля (в случае однородной, изотропной среды) соотношением
магнитного поля (в случае однородной, изотропной среды) соотношением
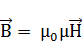
Магнитная индукция в центре кругового проводника (витка) с током
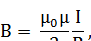
где R – радиус витка.
Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током,
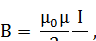
где r0 – расстояние от оси проводника.
Магнитная индукция поля, создаваемого отрезком проводника,
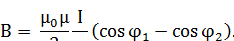
Обозначения ясны из рисунка 1.11а. Вектор индукции 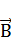 перпендикулярен плоскости чертежа, направлен к нам и поэтому изображен точкой.
перпендикулярен плоскости чертежа, направлен к нам и поэтому изображен точкой.
| Рисунок 1.11 – Магнитная индукция, создаваемая отрезком |
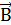
|
| r0 |
| φ1 |
| φ2 |
| I |
| I |
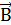
|
| r0 |
| φ |
| φ |
| а |
| б |
При симметричном расположении концов проводника относительно точки, в которой определяется магнитная индукция (рис. 1.11б), 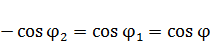 и, следовательно,
и, следовательно,
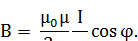
Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на оси),

где n – число витков, приходящихся на единицу длины соленоида; I – сила тока в одном витке.
Принцип суперпозиции магнитных полей: магнитная индукция 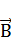 результирующего поля равна векторной сумме магнитных индукций
результирующего поля равна векторной сумме магнитных индукций 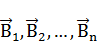 складываемых полей, т.е.
складываемых полей, т.е.
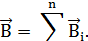
Магнитная индукция поля, создаваемого движущимся точечным зарядом Q в вакууме
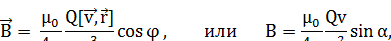
где  – скорость движущегося заряда;
– скорость движущегося заряда;  –радиус-вектор, направленный от заряда к точке, в которой определяется магнитная индукция
–радиус-вектор, направленный от заряда к точке, в которой определяется магнитная индукция 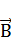 ; α – угол между векторами
; α – угол между векторами 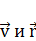 .
.
Механический момент, действующий на контур с током, помещенный в однородное магнитное поле,
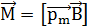 .
.
Дата добавления: 2015-02-13; просмотров: 1144;
