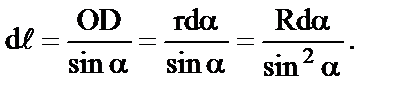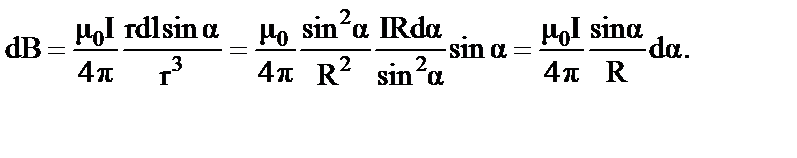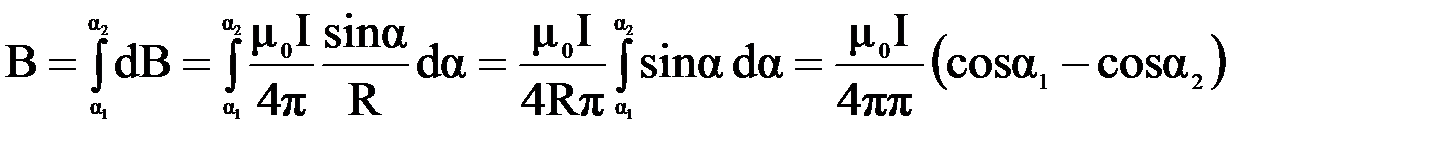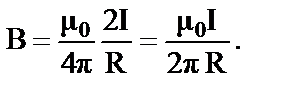Магнитное поле прямолинейного проводника с током
Представим себе ток, текущий по тонкому прямому проводу бесконечной длины (рис. 1.9). Возьмем произвольную точку А на расстоянии R от проводника. Согласно правилу правого винта (буравчика), векторы 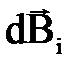 от
от
| Рисунок 1.9 - Магнитное поле прямолинейного проводника с током
|
каждого элемента тока dℓi имеют одинаковое направление, перпендикулярное плоскости чертежа (на нас).
Поэтому сложение векторов 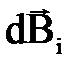 можно заменить сложением их модулей. При суммировании всех
можно заменить сложением их модулей. При суммировании всех 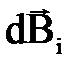 будет меняться угол α между r и dℓ, поэтому выберем α в качестве переменной интегрирования. Выразим через α все остальные величины, полагая, что отрезок АD ≈ r из-за малости dℓ. Итак, из треугольника АСЕ выразим r через известное нам расстояние R и переменную α:
будет меняться угол α между r и dℓ, поэтому выберем α в качестве переменной интегрирования. Выразим через α все остальные величины, полагая, что отрезок АD ≈ r из-за малости dℓ. Итак, из треугольника АСЕ выразим r через известное нам расстояние R и переменную α:
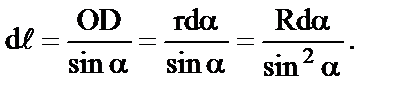
По закону Био-Савара-Лапласа получим:
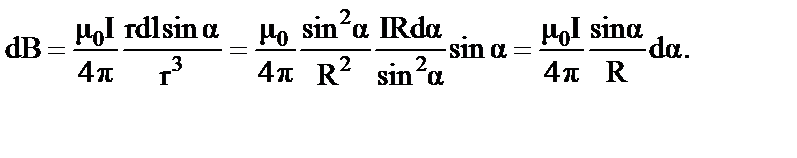
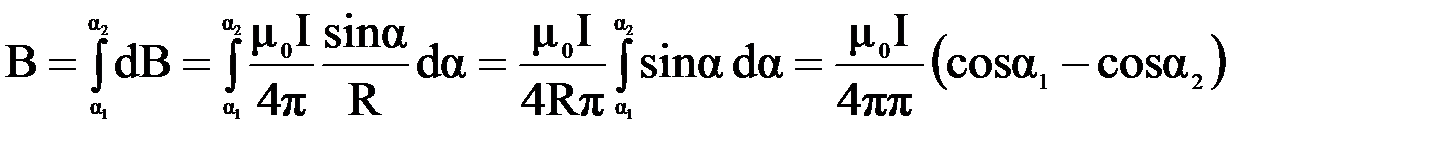
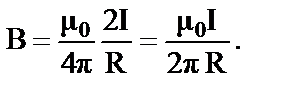
В данном выражении α1 и α2 - значения угла α для крайних точек проводника. Если прямолинейный проводник бесконечно длинный, то α1 = 0, α2 = π. Магнитная индукция в любой точке поля такого проводника с током:
Напомним, что линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей.
Дата добавления: 2015-02-13; просмотров: 1227;
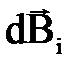 от
от 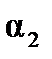
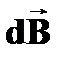
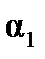
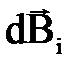 можно заменить сложением их модулей. При суммировании всех
можно заменить сложением их модулей. При суммировании всех 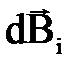 будет меняться угол α между r и dℓ, поэтому выберем α в качестве переменной интегрирования. Выразим через α все остальные величины, полагая, что отрезок АD ≈ r из-за малости dℓ. Итак, из треугольника АСЕ выразим r через известное нам расстояние R и переменную α:
будет меняться угол α между r и dℓ, поэтому выберем α в качестве переменной интегрирования. Выразим через α все остальные величины, полагая, что отрезок АD ≈ r из-за малости dℓ. Итак, из треугольника АСЕ выразим r через известное нам расстояние R и переменную α: