К расчету магнитного поля
Французские физики Ф. Савар и Ж.Б. Био изучали магнитное поле, создаваемое проводниками с постоянным током различной формы. На основании многочисленных опытов они пришли к выводу, что магнитная индукция поля проводника с током пропорциональна силе тока I, зависит от формы и размеров проводника, а также от расположения рассматриваемой точки по отношению к проводнику. Био и Савар пытались получить самый общий закон – для проводника любой формы и любой точки поля. Однако сделать это им не удалось. По их просьбе этой проблемой занялся французский математик П.С. Лаплас. Он высказал важную гипотезу о том, что при наложении магнитных полей справедлив принцип суперпозиции, т.е. принцип независимости действия полей. Если имеется несколько проводников с током, каждый из которых создает в исследуемой точке магнитное поле с индукциями 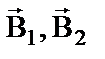 …, то результирующая магнитная индукция будет равна векторной сумме всех
…, то результирующая магнитная индукция будет равна векторной сумме всех 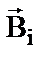 :
: 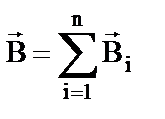 .
.
Если перейти к малым отрезкам провода с током, то суммирование надо заменить интегрированием и тогда индукция 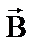 , создаваемая всем проводником с током I, будет равна:
, создаваемая всем проводником с током I, будет равна: 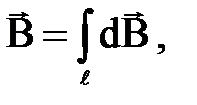 где
где 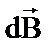 – индукция, создаваемая элементом длины проводника dℓ, интегрирование проводится по всей длине проводника.
– индукция, создаваемая элементом длины проводника dℓ, интегрирование проводится по всей длине проводника.
Лаплас обобщил экспериментальные результаты Био и Савара в виде дифференциального закона, называемого закономБио – Савара – Лапласа,
| Рисунок 1.7 - К закону Био-Савара-Лапласа |
|
| I |
|
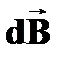
|
| A |
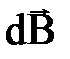 , создаваемая в некоторой точке А элементом проводника dℓ с током I, определяется формулой
, создаваемая в некоторой точке А элементом проводника dℓ с током I, определяется формулой
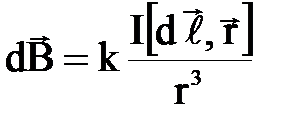
Выберем произвольную точку А вблизи проводника. Вектор 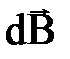 направлен в точке А перпендикулярно плоскости, построенной на векторах
направлен в точке А перпендикулярно плоскости, построенной на векторах  и
и 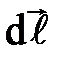 по правилу правого винта, и совпадает с направлением касательной к линии индукции в точке А (пунктирный круг) (рис.1.7). Коэффициент пропорциональности k зависит от выбора системы единиц. В СИ это размерная величина, равная μ0/4π, где μ0 - магнитная постоянная, равная 4π∙10-7 Гн/м.
по правилу правого винта, и совпадает с направлением касательной к линии индукции в точке А (пунктирный круг) (рис.1.7). Коэффициент пропорциональности k зависит от выбора системы единиц. В СИ это размерная величина, равная μ0/4π, где μ0 - магнитная постоянная, равная 4π∙10-7 Гн/м.
Таким образом, магнитную индукцию поля, создаваемую в вакууме током I, текущим по проводу конечной длины ℓ и любой формы, можно найти по формуле
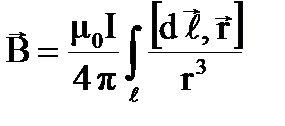
Дата добавления: 2015-02-13; просмотров: 1034;
