Закон Ампера

В 1820 г. А. Ампер установил, что сила, с которой магнитное поле действует на элементарный проводник с током I и длиной :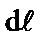

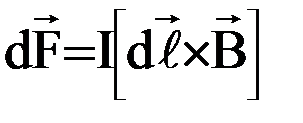Вектор 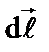совпадает по направлению с током. Данная формула выражает закон Ампера: сила, действующая на элемент проводника с током в магнитном поле, равна произведению силы тока на векторное произведение элемента длины проводника и магнитной индукции поля.

Рисунок 1.4 - Сила Ампера, действующая на проводник с током в магнитном поле

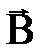
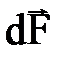
I

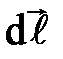
I

N

S

Если поместить проводник с током между полюсов постоянного магнита, то сила Ампера будет действовать на него в направлении, показанном на рис. 1.4.

Направление 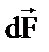может быть найдено по правилу левой руки: если ладонь левой руки расположить так, чтобы вектор 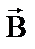был направлен в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отставленный под прямым углом большой палец укажет направление силы, действующей на элемент проводника с током(рис.1.5).

Модуль силы Ампера вычисляется по формуле 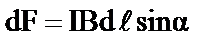, где α – угол между векторам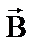и и 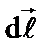. Чтобы найти силу, действующую на проводник конечной длины 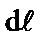в магнитном поле, необходимо определить геометрическую сумму сил, действующих на все малые элементы данного проводника,

т.е.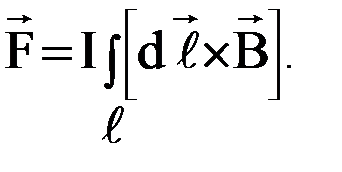

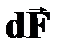
I

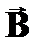
Рисунок 1.5 - Определение силы Ампера по правилу левой руки

Из закона Ампера следует, что магнитные силы нецентральные, так как они направлены перпендикулярно силовым линиям магнитного поля. Напомним, что электростатические силы – центральные.

Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера запишется в виде dF = IBdl, откуда .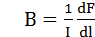

Единица магнитной индукции — тесла (Тл): 1 Тл — магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток 1 А: 1 Тл = 1 Н/(А м).

<123 4 5 6 7 >

Дата добавления: 2015-02-13; просмотров: 981;