Примеры решения задач. Задача 1.К тонкому однородному проволочному кольцу радиуса R подводят ток I
Задача 1.К тонкому однородному проволочному кольцу радиуса R подводят ток I. Подводящие провода, расположенные радиально, делят кольцо на две дуги, длины которых l1 и l2. Найти индукцию магнитного поля в центре кольца.
| l1 |
| l2 |
| I |
| r0 |
| I1 |
| I2 |
| Рисунок 1.12 - К задаче 1 |
| (1) |
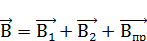 . (1)
. (1)
| (2) |
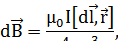
где d 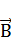 - вектор магнитной индукции поля, созданного элементом тока Id
- вектор магнитной индукции поля, созданного элементом тока Id  в точке, радиус – вектор которой
в точке, радиус – вектор которой  .
.
Токи в подводящих проводах не создают поля в центре кольца, так как для любого элемента d  , этих проводов [Id
, этих проводов [Id  ,
,  ]=0. Векторы индукции
]=0. Векторы индукции 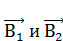
| (3) |
В=|B1-B2|,
| (4) |
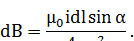
В центре кольца для каждого элемента тока r = r0; 
Все элементарные 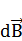 полей, созданных элементами тока
полей, созданных элементами тока 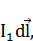 коллинеарны между собой, и интегрирование выражения (4) по дуге l1 дает
коллинеарны между собой, и интегрирование выражения (4) по дуге l1 дает
| (5) |
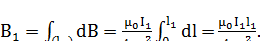
Аналогично,
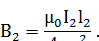
Подставляя выражения для B1 и B2 в (3) получаем

Соединение проводников l1 и l2– параллельное, сопротивление каждого из них прямо пропорционально длине (по условию, кольцо однородное). Это значит, что силы токов I1 и I2обратно пропорциональны сопротивлениям R1 и R2, т.е. обратно пропорциональны длинам дуг l1 и l2:
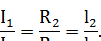
Следовательно, I1l1 = I2l2, и индукция магнитного поля в центре кольца B = 0.
Очевидно, что если в выражении (5) заменить длину дуги l1 длиной окружности l = 2πr0, то получается известное выражение индукции в центре витка, обтекаемого током I1:
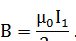
Задача 2.По двум длинным прямолинейным проводам, находящимся на расстоянии r = 5 см друг от друга в воздухе, текут токи I = 10 A каждый. Определить магнитную индукцию B поля, создаваемого токами в точке, лежащей посередине между проводами, для случаев:
1) Провода параллельны, токи текут в одном направлении (рис. 1.13а);
2) Провода параллельны, токи текут в противоположных направлениях (рис. 1.13б);
3) Провода перпендикулярны, направление токов указано на рис. 1.13в.
Решение: Результирующая индукция магнитного поля равна векторной
сумме:  ,где
,где 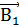 – индукция поля, создаваемого током I1;
– индукция поля, создаваемого током I1;  –индукция поля, создаваемого током I2.
–индукция поля, создаваемого током I2.
| б |
| B1 |
| B2 |
| I2 |
| + |
| + |
| I1 |
| B1 |
| B2 |
| I2 |
| • |
| I1 |
| + |
| I2 |
| I1 |
| в |
| B2 |
| B |
| B1 |
| a |
| Рисунок 1.13 – К задаче 2 |
| (6) |
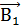 и
и 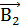 направлены по одной прямой, то векторная сумма может быть заменена алгебраической суммой:
направлены по одной прямой, то векторная сумма может быть заменена алгебраической суммой:
B = B1+B2.
При этом слагаемые B1 и B2 должны быть взяты с соответствующими знаками.
| (7) |
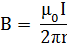
Подставив значения величин в формулу (6), найдем модули 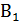 и
и  :
:
B1=B2= 80 мкТл.
1-й случай. Векторы 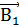 и
и 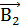 направлены по одной прямой (рис. 1.13а); следовательно, результирующая индукция
направлены по одной прямой (рис. 1.13а); следовательно, результирующая индукция 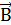 определяется по формуле (6). Приняв направление вверх положительным, вниз – отрицательным, получим:
определяется по формуле (6). Приняв направление вверх положительным, вниз – отрицательным, получим:
B = B1+B2 = -80 мкТл+80 мкТл=0.
2-й случай. Векторы 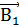 и
и 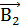 направлены по одной прямой в одну сторону (рис. 1.13б).поэтому можем записать
направлены по одной прямой в одну сторону (рис. 1.13б).поэтому можем записать
B = B1+B2 = -80 мкТл -80 мкТл= -160 мкТл.
3-й случай. Векторы индукций магнитных полей, создаваемых токами в точке, лежащей посередине между проводами, взаимно перпендикулярны (рис. 1.13в). Результирующая индукция по модулю и направлению является диагональю квадрата, построенного на векторах 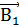 и
и 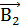 . По теореме Пифагора найдем
. По теореме Пифагора найдем
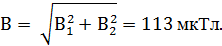
Задача 3.Бесконечно длинный проводник изогнут так, как это изображено на рис. 1.14а. радиус дуги окружности R = 10 см. Определить магнитную индукцию 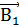 поля, создаваемого в точке O током I = 80 А, текущим по этому проводнику.
поля, создаваемого в точке O током I = 80 А, текущим по этому проводнику.
| б |
| а |
| I |
| O |
| R |
| O |
| I |
| α1 |
| α2 |
| π |
| B = B1 + B2 + B3 |
| Рисунок 1.14 – К задаче 3 |
Решение: Магнитную индукцию 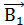 в точке O найдем, используя принцип суперпозиции магнитных полей
в точке O найдем, используя принцип суперпозиции магнитных полей 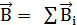 . В нашем случае проводник можно разбить на три части (рис. 1.14б): два прямолинейных проводника (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда
. В нашем случае проводник можно разбить на три части (рис. 1.14б): два прямолинейных проводника (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда
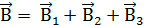 ,
,
где 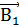 ,
,  и
и 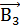 – магнитные индукции поля в точке O, создаваемые током, текущим соответственно на первом, втором и третьем участках проводника.
– магнитные индукции поля в точке O, создаваемые током, текущим соответственно на первом, втором и третьем участках проводника.
Так как точка O лежит на оси проводника 1, то B1 = 0 и тогда
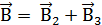
Учитывая, что векторы 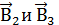 направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, геометрическое суммирование можно заменить алгебраическим:
направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, геометрическое суммирование можно заменить алгебраическим:
B = B2 + B3.
Магнитную индукцию поля B2 можно найти, используя выражение для магнитной индукции в центре кругового проводника с током I:
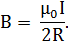
Так как магнитная индукция B2 создается в точке O половиной такого кругового проводника с током, то, учитывая равный вклад в магнитную индукцию от каждой половинки проводника, можно написать
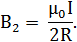
Магнитную индукцию B3 найдем, используя формулу
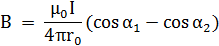
В нашем случае r0 = R, α1 =  (cosα1 = 0),
(cosα1 = 0),  (cosα2 = -1). Тогда
(cosα2 = -1). Тогда
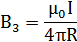
Используя найденные выражения для B2 и B3, получим
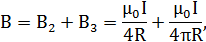
или
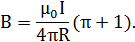
Произведем вычисления: B = 3.31∙10-4Тл = 331 мкТл.
Задача 4.По двум параллельным прямым проводам длиной l = 2,5 м каждый, находящимся на расстоянии d = 20 см друг от друга, текут одинаковые токи I = 1 кА. Вычислить силу F взаимодействия токов.
Решение: Взаимодействие двух проводников, по которым текут токи, осуществляется через магнитное поле. Каждый ток создает магнитное поле, которое действует на другой проводник. Предположим, что оба тока (обозначим их I1 и I2) текут в одном направлении (рис. 1.15).
Вычислим силу F1,2, с которой магнитное поле, созданное током I1, действует на проводник с током I2. Для этого проведем магнитную силовую
| I1 |
| I2 |
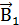
|
| dl2 |
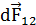
|
| Рисунок 1.15 – К задаче 4 |
| (8) |
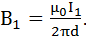
| (9) |
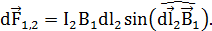
Так как отрезок d 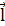 перпендикулярен вектору
перпендикулярен вектору 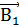 , то
, то
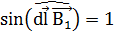 .
.
И тогда
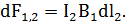
Подставив в выражение (9) B1 из (8), получим
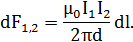
Силу F1, 2 взаимодействия проводников с током найдем интегрированием по всей длине второго проводника:
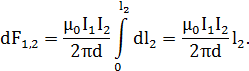
Заметив, что I1 = I2 =I и l2 = l, получим
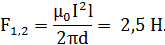
Сила 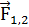 сонаправлена с силой
сонаправлена с силой 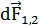 (рисунок 1.15) и определяется правилом левой руки.
(рисунок 1.15) и определяется правилом левой руки.
Задача 5.Провод в виде тонкого полукольца радиусом R=10см находится в однородном магнитном поле (В=50мТл). По проводу течет ток I=10А. Найти силу 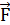 , действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а проводящие провода находятся вне поля.
, действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а проводящие провода находятся вне поля.
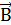
|
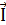
|
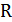
|
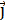
|
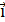
|

|

|
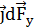
|
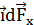
|
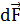
|
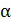
|
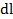
|
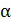
|
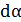
|
| Рисунок 1.16 – К задаче 5 |
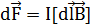 . Направление этой силы можно определить по правилу векторного произведения или по правилу левой руки.
. Направление этой силы можно определить по правилу векторного произведения или по правилу левой руки.
Используя симметрию, выберем координатные оси так, как это изображено на рисунке. Силу 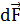 представим в виде
представим в виде
 ,
,
где 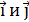 –единичные векторы (орты); dFx и dFy – проекции вектора
–единичные векторы (орты); dFx и dFy – проекции вектора  на координатные оси Оx и Оy.
на координатные оси Оx и Оy.
Силу 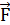 , действующую на весь провод, найдем интегрированием:
, действующую на весь провод, найдем интегрированием:

где символ L указывает на то, что интегрирование ведется по всей длине провода L.
Из соображений симметрии первый интеграл (  ) равен нулю.
) равен нулю.
Тогда
| (10) |

Из рисунка следует, что
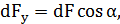
где dF – модуль вектора  (
( 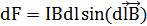 ). Так как вектор
). Так как вектор 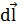 перпендикулярен вектору
перпендикулярен вектору 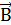 (
( 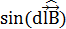 = 1), то dF = IBdl. Выразив длину дуги dl через радиус R и угол α , получим
= 1), то dF = IBdl. Выразив длину дуги dl через радиус R и угол α , получим
dF= IBR dα.
Тогда
dFy= IBR cosα dα.
Введем dFy под интеграл соотношения (10) и проинтегрируем в пределах от
-π/2 до +π/2 (как это следует из рисунка):
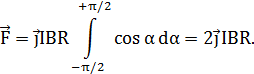
Из полученного выражения видно, что сила 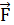 сонаправлена с положительным направлением оси Оy (единичным вектором
сонаправлена с положительным направлением оси Оy (единичным вектором 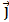 ).
).
Модуль силы :F= | 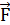 | = 2 IBR = 0,1H.
| = 2 IBR = 0,1H.
Задача 6.На проволочный виток радиусом r= 10 см, помещенный между полюсами магнита, действует максимальный механический момент Мmax=6,5 мкН. Сила тока I в витке равна 2А. Определить магнитную индукцию В поля между полюсами магнита. Действием магнитного поля Земли пренебречь.
| (11) |
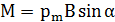 .
.
Если учесть, что максимальное значение механический момент принимает при 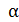 =
= 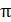 /2 (
/2 ( 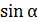 =1), а также, что
=1), а также, что 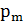 =IS, то формула(11) примет вид
=IS, то формула(11) примет вид
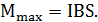
Отсюда, учитывая, что 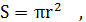 находим
находим
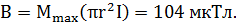
Вывод:Закон Био–Савара–Лапласа, а следовательно, и формулы, выведенные с его помощью, справедливы только для линейных токов (т.е. токов, текущих по проводникам, поперечные размеры которых пренебрежимо малы).
Контрольные вопросы второго уровня (сборник задач)
1. По двум параллельным одинаковым проводам текут в противоположных направлениях токи силой I1= 10 А и I2= 15 А. Расстояние между проводами 10 см. Определите индукцию магнитного поля в точке, удаленной от первого провода на r1 = 8 см и г2 = 6 см от второго провода. [56 мкТл]
2. По двум длинным параллельным проводникам, находящимся на расстоянии l= 5 см друг от друга, текут в одном направлении токи силой I1= I2= 10 А. Определите индукцию магнитного поля в точке, удаленной от каждого проводника на расстояние r= 3 см. [0,11 мТл]
3. В прямом проводе длиной l=0,1 м сила тока I=6 А. Определите напряженность магнитного поля в точке, лежащей на расстоянии r= 0,5 м от середины провода. [1,35 А/м]
4. По бесконечной прямолинейной тонкостенной трубе радиусом Rтечет ток. Определите индукцию магнитного поля в произвольной точке внутри трубы, если сила тока равна I. [μ0I/(π2R)]
5. Определите индукцию магнитного поля посредине между длинными параллельными проводниками на расстоянии r= 10 см один от другого, выразив ее через силу тока I в одном из проводников, если по другому проводнику течет ток I1= 10 А в том же направлении, что и в первом проводнике. [В=4∙10 – 6 (10 - I)]
6. Два круговых витка расположены во взаимно перпендикулярных плоскостях так, что их центры совпадают. Найдите индукцию в центре витков, если радиусы витков одинаковы R = 5 см, и сила тока в каждом витке I = 2 А. [35 мкТл]
7. К кольцу из медной проволоки, площадь сечения которой S= 1 мм2, приложено напряжение U=0,15 В. При этом сила тока в кольце I = 10 А. Найдите индукцию магнитного поля и центре кольца. [44,7 мкТл]
8. По двум длинным параллельным проводникам, расположенным на расстоянии d один от другого, текут токи в одном направлении (I1 = 2I2). Выразите зависимость магнитной индукции В от х, где х — расстояние вдоль перпендикуляра между проводниками. Первый из проводников находится при х = 0, другой — при х = d. 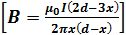
9. Бесконечно длинный прямой проводник согнут под прямым углом. По проводнику течет ток I = 100 А. Вычислите магнитную индукцию в точках, лежащих на биссектрисе угла и удаленных от вершины угла на а= 10 см. [482 мкТл; 82 мкТл]
10. По бесконечно длинному прямому проводнику, согнутому под углом α = 120°, течет ток I = 50 А. На сколько отличаются значения магнитной индукции в точках, лежащих на биссектрисе угла и удаленных от его вершины на расстояние a = 5см. [ΔB = 230 мкТл]
11. По контуру в виде равностороннего треугольника течет ток I = 40 А. Найдите длину стороны треугольника, если магнитная индукция в точке пересечения высот 240 мкТл. [30 см]
12. По тонкому проводу, изогнутому в виде прямоугольника, течет ток. Стороны прямоугольника а = 30 см и b = 40 см. Какова сила тока, если магнитная индукция в точке пересечения диагоналей 200 мкТл? [60 А]
13. Тонкий провод изогнут в виде правильного шестиугольника. Стороны шестиугольника а = 5 см. Определите магнитную индукцию в центре шестиугольника, если по нему течет ток I = 10 А. [139 мкТл]
14. По двум бесконечно длинным параллельным проводам протекают токи в противоположных направлениях, причем I1 = 2I2. Расстояние между ними равно d. Определите положение точек, в которых индукция магнитного поля равна нулю. [На расстоянии х = d от тока I2]
15. Молния ударяет в железный флагшток высотой h = 7,0 м и диаметром d = 9,8 см, причем электроны движутся вверх по флагштоку. Разность потенциалов между вершиной и основанием флагштока равна U=20 кВ. Какие величину и направление имеет индукция магнитного поля на расстоянии 50 см к северу от флагштока? [88 Тл, на восток]
16. По обмотке очень короткой катушки радиусом r = 16 см течет ток силой I=5А. Сколько витков n проволоки намотано на катушку, если напряженность магнитного поля в ее центре Н= 800 А/м? [51]
17. Увеличится или уменьшится индукция В в центре квадратной рамки, по которой течет ток I, если квадрат превратить в окружность? [Уменьшится]
18. Из куска изолированной проволоки сделан круглый виток радиусом R и подключен к источнику тока с постоянной ЭДС. Как изменится индукция магнитного поля в центре круга, если из того же куска проволоки сделать два прилегающих друг к другу витка радиусом R/2? [Увеличится в 4 раза]
19. Индукция магнитного поля в центре соленоида длиной 32 см и диаметром 1,2 см должна составлять 0,20 Тл. Сколько витков должна иметь обмотка, если сила тока в ней не может превышать 3,7 А? [13 772]
20. Бесконечно длинный тонкий проводник с током I = 50A имеет изгиб (плоскую петлю) радиусом R = 10 см. Определить в точке O магнитную индукцию В поля, создаваемого этим током, в случаях a-e, изображенных на рисунке 1.17.
| а |
| б |
| г |
| д |
| R |
| O |
| I |
| O |
| R |
| I |
| R |
| I |
| O |
| O |
| R |
| I |
| O |
| R |
| I |
| O |
| R |
| I |
| в |
| Рисунок 1.17 – К задаче 20 |
| е |
[а) 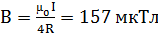 ; б)
; б) 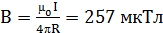 ; в)
; в) 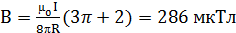 ; г)
; г) 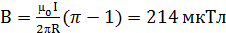 ;д)
;д) 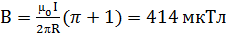 ; е)
; е)  ]
]
21.
| а |
| б |
| в |
| г |
| д |
| е |
| 2R |
| O |
| I |
| R |
| 2R |
| I |
| O |
| R |
| 2R |
| I |
| 2π/3 |
| R |
| I |
| 2π/3 |
| R |
| I |
| O |
| R |
| R |
| I |
| R |
| O |
| Рисунок 1.18 – К задаче 21 |
[а) 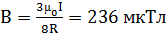 ; б)
; б) 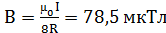 ; в)
; в) 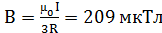 ;
;
г) 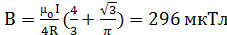 ; д)
; д) 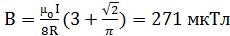 ; е)
; е) 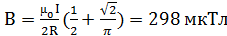 ]
]
22. Электрон в невозбужденном атоме водорода движется вокруг ядра по окружности с радиусом r = 53 пм. Вычислить силу эквивалентного кругового тока I и напряженность H поля в центре окружности. [1,1 мА; 10 МА/м]
23. На расстоянии r = 10 нм от траектории прямолинейно движущегося электрона максимальное значение магнитной индукции В= 160 мкТл. Определите скорость электрона. [106 м/с]
24. Определить максимальную магнитную индукцию Bmax поля, создаваемого электроном, движущимся прямолинейно со скоростью v = 107 м/с, в точке, отстоящей от траектории на расстоянии d = 1 нм.[16 мТл]
25. В однократно ионизированном атоме гелия электрон движется по круговой орбите радиуса r = 26,5 пм со скоростью v = 4,36 Мм/с. Определить по модулю и направлению магнитную индукцию 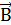 поля, создаваемого ядром атома гелия в точке, совпадающей с движущимся электроном. [
поля, создаваемого ядром атома гелия в точке, совпадающей с движущимся электроном. [ 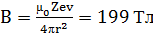 ]
]
26. Очень короткая катушка содержит 100 витков тонкого провода. Катушка имеет квадратное сечение со стороной а = 5 см. Найдите магнитный момент катушки при токе I = 10 А. [2,5 А . м2]
27. По тонкому стержню длиной l = 30 см равномерно распределен заряд q = 120 нКл. Стержень приведен во вращение с постоянной угловой скоростью ω = 10 рад/с относительно оси, перпендикулярной стержню и проходящей через его середину. Определите магнитный момент, обусловленный вращением заряженного стержня. [4,5 нА  м2]
м2]
28. Тонкое кольцо радиусом R =10 см, несущее заряд q= 10 нКл, равномерно вращается относительно оси, перпендикулярной плоскости кольца и проходящей через его центр. Магнитный момент, обусловленный вращением заряженного кольца, рm = 3,14 нА•м2. С какой частотой вращается кольцо? [10 об/с]
29. Рамка гальванометра, содержащая N=200 витков тонкого провода, подвешена на упругой нити. Площадь S рамки равна 1 см2. Нормаль к плоскости рамки перпендикулярна линиям магнитной индукции (В = 5 мТл). Когда через гальванометр был пропущен ток I = 2 мкА, то рамка повернулась на угол  = 30°. Найти постоянную кручения G нити. [332 пН∙м/рад]
= 30°. Найти постоянную кручения G нити. [332 пН∙м/рад]
30. На оси контура с током, магнитный момент которого pm = 10 мА∙м2, находится другой такой же контур. Вектор магнитного момента второго контура перпендикулярен оси. Вычислить механический момент М, действующий на второй контур. Расстояние d между контурами равно 50 см. Размеры контуров малы по сравнению с расстоянием между ними. [160 пН∙м]
Контрольные вопросы третьего уровня (тесты)
1.По проводнику АБ, помещенному в магнитное поле, течет ток. Потенциал точки Б больше потенциала точки А, направление силы Ампера указано на рисунке. Определить направление вектора индукции.
 1) перпендикулярно плоскости рисунка 2) влево
1) перпендикулярно плоскости рисунка 2) влево
3) вправо 4) вниз 5) вверх
2.Прямой провод, по которому течет постоянный ток, расположен в однородном магнитном поле перпендикулярно линиям магнитной индукции. Если длину провода увеличить в два раза, а силу тока в нем уменьшить в четыре раза, во сколько раз изменится сила Ампера?
1) уменьшится в 2 раза; 2) увеличится в 4 раза; 3) увеличится в 2 раза; 4) уменьшится в 4 раза; 5) увеличится в 8 раз.
3.  По проводнику АБ протекает постоянный ток. Проводник помещен в однородное магнитное поле, линии индукции которого перпендикулярны проводнику (см. рис.). Потенциал точки А больше потенциала точки Б. Определить направление силы Ампера, действующей на проводник.
По проводнику АБ протекает постоянный ток. Проводник помещен в однородное магнитное поле, линии индукции которого перпендикулярны проводнику (см. рис.). Потенциал точки А больше потенциала точки Б. Определить направление силы Ампера, действующей на проводник.
1) вверх 2) вниз 3) влево 4) вправо 5) вдоль линий индукции
4.Какая формула определяет закон Ампера?
1. 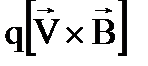 2.
2. 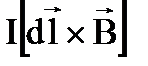 3.
3. 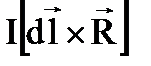 4.
4. 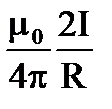 5.
5. 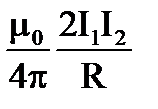
|
6. Какая формула определяет магнитный момент 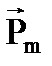 контура с током?
контура с током?
1.  2.
2. 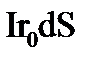 3.
3. 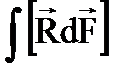 4.
4. 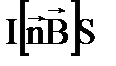 5.
5. 
7.Линиями магнитной индукции называются линии:
1) по которым текут токи; 2) касательные к которым в каждой точке совпадают с направлением напряженности поля; 3) касательные к которым в каждой точке совпадают с направлением индукции поля;
4) замкнутые; 5) равного потенциала.
| 8. Магнитный момент Рmконтура с током ориентирован во внешнем магнитном поле Bтак, как показано на рисунках. Положение рамки устойчиво и момент сил, действующих на нее, равен нулю в случае ... | ||||
| 1. | 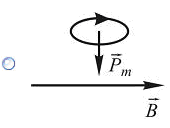
| 2. | 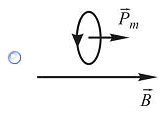
| |
| 3. | 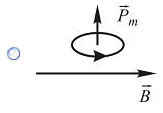
| 4. | 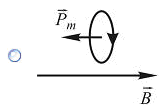
| |
| 9. Рамка с током с магнитным моментом, направление которого указано на рисунке, находится в однородном магнитном поле. Момент сил, действующих на рамку, направлен... |
| ||
| 1. | Против вектора магнитной индукции | ||
| 2. | Противоположно вектору магнитной индукции | ||
| 3. | Перпендикулярно плоскости рисунка к нам | ||
| 4. | Перпендикулярно плоскости рисунка от нас | ||
10. Какая формула определяет магнитную индукцию поля прямого тока?
1. 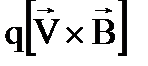 2.
2. 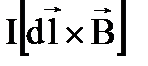 3.
3. 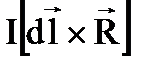 4.
4. 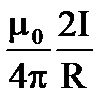 5.
5. 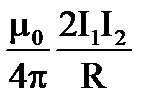
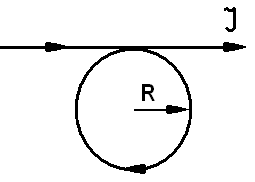 11. Чему равна индукция поля в центре кольца, изображенного на рисунке?
11. Чему равна индукция поля в центре кольца, изображенного на рисунке?
1. 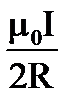 2.
2. 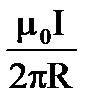 3.
3. 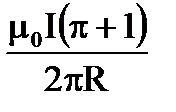 4.
4. 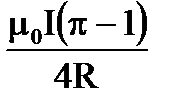
5. 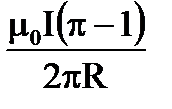
12. Как записывается теорема Гаусса для вектора индукции магнитного поля?
1. 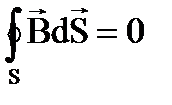 2.
2. 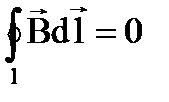 3.
3.  4.
4. 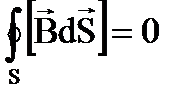 5.
5. 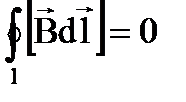
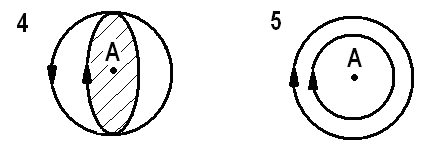
13. В каком случае индукция поля, созданного двумя кольцевыми токами в точке А, будет наибольшей?

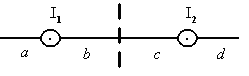
| 14. На рисунке изображены сечения двух прямолинейных проводников с токами I1 < I2. Индукция Врезультирующего магнитного поля равна нулю в некоторой точке интервала... |
| ||||||||
| 1. | b | 2. | с | 3. | d | 4. | a | ||
15. Какая формула определяет поле в центре кругового тока?
1. 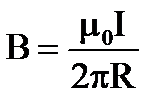 2.
2. 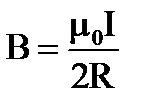 3.
3. 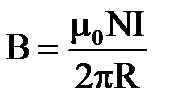 4.
4. 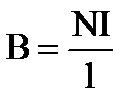 5.
5. 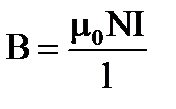
| 16. Бесконечно длинный проводник с током, согнутый под прямым углом, создает в точке А магнитное поле с индукцией В = 0,12 Тл. Индукция магнитного поля, создаваемого горизонтальной частью проводника, в точке Аравна ... | 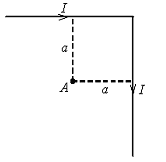
| |||
1. 0,03 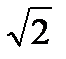 Тл Тл
| 2. | 0,06 Тл | ||
3. 0,06 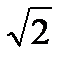 Тл Тл
| 4. | 0,08 Тл | ||
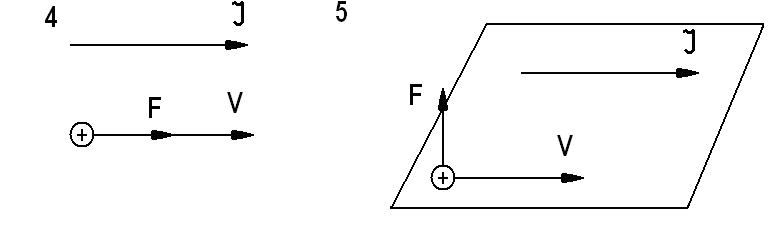
17. На каком рисунке правильно показано направление силы F, действующей на положительный заряд, движущийся параллельно прямому току I?

| 18. Магнитное поле создано двумя параллельными проводниками с токами I1 и I2, расположенными перпендикулярно плоскости чертежа. Если I1 = 2I2, то вектор B индукции результирующего поля в точке А направлен... | 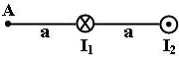
| |||||||
| 1. | Вверх | 2. | Влево | 3. | Вправо | 4. | Вниз | |
| 19. На рисунке изображен вектор скорости движущегося протона. Вектор магнитной индукции Bполя, создаваемого протоном при движении, в точке С направлен ... | 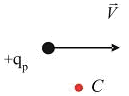
| |||||||||
| 1. | Слева направо | 2. | От нас | 3. | Снизу вверх | 4. | Сверху вниз | 5. | На нас | |
20. Какая формула определяет силу взаимодействия двух бесконечных параллельных токов?
1. 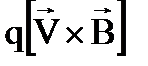 2.
2. 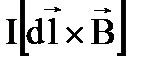 3.
3. 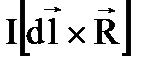 4.
4. 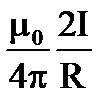 5.
5. 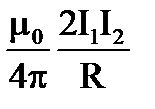
Дата добавления: 2015-02-13; просмотров: 10535;

