Пересечение прямой линии с плоскостью
Это есть позиционная задача, т.к. в ней определяется общий элемент данных геометрических объектов, т.е. их точка пересечения, что соответствует рисунку 1.3.24.
Алгоритм решения задачи основывается на следующем способе:
1) через прямую линию проводят вспомогательную проецирующую плоскость-посредник;
2) находят линию пересечения вспомогательной плоскости с данной
плоскостью;
3) отмечают точку пересечения полученной линии с данной прямой;
4) определяют видимость прямой относительно даной плоскости.
Через прямую а, которая пересекает плоскость общего положения, заданная треугольником АВС, в соответствии с рисунком 1.3.24 проведена вспомогательная фронтально проецирующая плоскость Q(Q2), обозначенная на чертеже Q2ºа2.
Линией пересечения b плоскости Q с заданной плоскостью треугольника АВС является прямая линия. Эта линия строится с помощью точек 1 и 2. Первоначально отмечаем фронтальные проекции 12 и 22 этих точек в пересечении следа Q2 плоскости 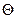 с фронтальными проекциями А2В2 и А2С2 соответствующих сторон треугольника АВС. Затем по свойству принадлежности определяем горизонтальные проекции точек 1 и 2 на горизонтальных проекциях этих сторон.
с фронтальными проекциями А2В2 и А2С2 соответствующих сторон треугольника АВС. Затем по свойству принадлежности определяем горизонтальные проекции точек 1 и 2 на горизонтальных проекциях этих сторон.
Пересечение линии b1 c линией a1 определяет горизонтальную проекцию К1 искомой точки К. Фронтальная проекция К2 точки К получается в пересечении линии связи, проведённой из точки К1 с линией a2.
Видимость прямой а относительно плоскости треугольника АВС определена с помощью конкурирующих точек 1, 1¢ и 3, 3¢.

 Рисунок 1.3.24 – Пересечение прямой линии с плоскостью
Рисунок 1.3.24 – Пересечение прямой линии с плоскостью
Дата добавления: 2015-02-13; просмотров: 797;
