При граничных условиях 1 рода

Дифференциальное уравнение теплопроводности при стационарном режиме для одномерного температурного поля имеет вид

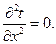(75)

Дважды интегрируя это уравнение, получим последовательно:

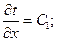
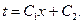(76)

Из уравнения (76) следует, что распределение температуры по толщине плоской стенки при стационарном тепловом режиме осуществляется по прямой линии.

Уравнение (76) есть общее решение уравнения (75). Задав температуры внутренней t_вн и наружной t_н поверхностей (частный случай граничных условий 1 рода), можно найти значения постоянных С₁ и С₂.

При x = 0 t_c1 = t_вн. Из уравнения (76) находим C₂ = t_вн.

При x = d t_c2 = t_н, тогда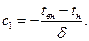

Следовательно, уравнение (76) будет иметь вид

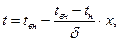(77)

где d - толщина стенки.

Уравнение (77) позволяет определить температуру в любой точке по толщине стенки при условии l = const.

Для определения плотности теплового потока, проходящего через плоскую стенку путем теплопроводности, используется закон Фурье (42).

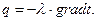
Так как 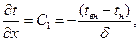то

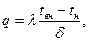(78)

Коэффициент теплопроводности 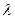- количество теплоты, переданное через единицу поверхности в единицу времени при градиенте температур один градус на единицу толщины стенки.

Размерность l [Вт/(м град)] выводится из уравнения (78)

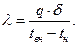
Отношение 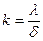называется тепловой проводимостью стенки, ее размерность Вт/(м²∙град).

Отношение 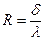называется внутренним тепловым (термическим) сопротивлением стенки, оно имеет размерность (м²∙град)/Вт.

Из уравнения (78)

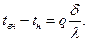(79)

Совместное решение уравнений (77) и (79) позволяет получить еще одну формулу для определения температуры в любой точке тела при стационарном тепловом состоянии при l = const.

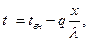(80)

где 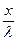- внутреннее тепловое сопротивление слоя стенки на

расстоянии x от начала координат, м² град/Вт.

Если стенка (кладка печи) многослойная, то плотность теплового потока, передаваемого от внутренней поверхности стенки к наружной, следует рассчитывать по формуле:

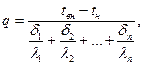(81)

где 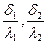– внутренние тепловые сопротивления отдельных слоев

стенки, имеющих различные величины коэффициента

теплопроводности.

Температура на границе между слоями может быть определена по формуле

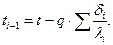(82)

Если теплота передается через цилиндрическую стенку, необходимо учитывать ее длину 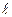, и тепловой поток определяется согласно закону Фурье либо общий (Вт)

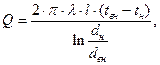(83)

либо отнесенный к одному погонному метру длины (Вт/м), называемый линейной плотностью теплового потока:

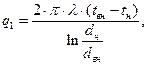(84)

либо отнесенный к единице площади внутренней или наружной поверхности стенки

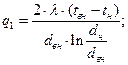(85)

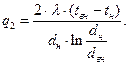(86)

Изменение температуры по толщине разделительной стенки происходит по логарифмическому закону

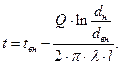(87)

Если температура наружной поверхности стенки (кладки печи) выше температуры окружающей среды, то будет происходить процесс отвода теплоты с поверхности стенки излучением и свободной конвекцией, причем при стационарном режиме тепловой поток, передаваемый теплопроводностью, должен быть равен сумме тепловых потоков, передаваемых с поверхности излучением и конвекцией:

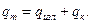(88)

Плотность теплового потока, переданного от наружной поверхности стенки излучением, определяется по формуле (41) Стефана-Больцмана.

Движение воздуха при свободной конвекции осуществляется под действием разности плотностей холодного и нагретого воздуха в поле действия массовых сил (сил земного притяжения). Передача теплоты свободной конвекцией рассчитывается по формуле Ньютона-Рихмана (39) и выражению (64).