Пример расчета нагревания массивного тела
Условие. Металлическая заготовка в форме цилиндра диаметром 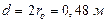 с начальной температурой
с начальной температурой 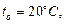 нагревается в печи, температура которой
нагревается в печи, температура которой 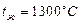 поддерживается постоянной. Коэффициент теплоотдачи
поддерживается постоянной. Коэффициент теплоотдачи 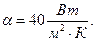 Нагревание производится до заданной температуры по оси заготовки
Нагревание производится до заданной температуры по оси заготовки  . Материал – сталь.
. Материал – сталь.
Таблица 6
Коэффициенты для расчета охлаждения (нагревания) пластины толщиной 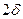
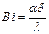
| 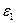
| 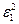
| 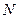
| 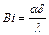
| 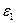
| 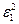
| 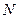
|
| 0,00 | 0,0000 | 0,0000 | 1,000 | 0,55 | 0,6800 | 0, 462 | 1,076 |
| 0,01 | 0,0998 | 0,0100 | 1,002 | 0,60 | 0,705 1 | 0,497 | 1,081 |
| 0,02 | 0,1410 | 0,0199 | 1,003 | 0,70 | 0,7506 | 0,564 | 1,092 |
| 0,04 | 0,1987 | 0,0397 | 1,006 | 0,80 | 0,7910 | 0,626 | 1,102 |
| 0,06 | 0,2425 | 0,0584 | 1,010 | 0,90 | 0,8274 | 0,684 | 1,111 |
| 0,08 | 0,2791 | 0,0778 | 1,013 | 1,00 | 0,8603 | 0,740 | 1,119 |
| 0,10 | 0,3111 | 0,0968 | 1,016 | 1,20 | 0,9171 | 0,841 | 1,134 |
| 0,12 | 0,3397 | 0,1154 | 1,020 | 1,40 | 0,9649 | 0,931 | 1,148 |
| 0,14 | 0,3656 | 0,1337 | 1,023 | 1,60 | 1,0008 | 1,016 | 1,159 |
| 0,16 | 0,3896 | 0,1518 | 1,026 | 1,80 | 1,0440 | 1,090 | 1,169 |
| 0,18 | 0,4119 | 0,1697 | 1,029 | 2,00 | 1,0769 | 1,160 | 1,179 |
| 0 20 | 0,4328 | 0,1874 | 1,031 | 2,2 | 1,1054 | 1,222 | 1,186 |
| 0,22 | 0,4525 | 0,2048 | 1,034 | 2,4 | 1,1300 | 1,277 | 1,193 |
| 0,24 | 0,4712 | 0,2220 | 1,037 | 2,6 | 1,1541 | 1,332 | 1,200 |
| 0,26 | 0,4889 | 0,2390 | 1,040 | 2,8 | 1,1747 | 1,380 | 1,205 |
| 0,28 | 0,5058 | 0,2558 | 1,042 | 3,0 | 1,1925 | 1,420 | 1,210 |
| 0,30 | 0,5218 | 0,2723 | 1,045 | 3,5 | 1,2330 | 1,52 | 1,221 |
| 0,35 | 0,5590 | 0,3125 | 1,052 | 4,0 | 1,2646 | 1,59 | 1,229 |
| 0,40 | 0,5932 | 0,3516 | 1,058 | 4,5 | 1,2880 | 1,66 | 1,235 |
| 0,45 | 0,6240 | 0,3894 | 1,064 | 5,0 | 1,3138 | 1,73 | 1,240 |
| 0,50 | 0,6533 | 0,4264 | 1,070 | 5,5 | 1,3340 | 1,78 | 1,244 |
Таблица 7
Коэффициенты для расчета охлаждения (нагревания)
длинного цилиндра радиусом 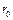
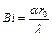
| 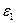
| 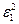
| 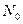
| 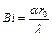
| 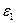
| 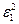
| 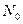
|
| 0,00 | 0,0000 | 0,0000 | 1,000 | 0,55 | 0,98081 | 0,962 | 1,124 |
| 0,01 | 0,1412 | 0,0200 | 1,002 | 0,60 | 1,0184 | 1,036 | 1,134 |
| 0,02 | 0,1995 | 0,0398 | 1,005 | 0,70 | 1,08731 | 1,184 | 1,154 |
| 0,04 | 0,2814 | 0,0792 | 1,010 | 0,80 | 1,1490 | 1,322 | 1,1721 |
| 0,06 | 0,3438 | 0,1183 | 1,014 | 0,90 | 1,2048 | 1,453 | 1,190 |
| 0,08 | 0,3960 | 0,1569 | 1,019 | 1,00 | 1,2558 | 1,580 | 1,2081 |
| 0,10 | 0,4417 | 0,1951 | 1,024 | 1,20 | 1,3450 | 1,81 | 1,239 |
| 0,12 | 0,4726 | 0,2329 | 1,029 | 1,40 | 1,4250 | 2,03 | 1,268 |
| 0,14 | 0,5200 | 0,2704 | 1,034 | 1,60 | 1,4900 | 2,22 | 1,295 |
| 0,16 | 0,5545 | 0,3075 | 1,039 | 1,80 | 1,5460 | 2,39 | 1,319 |
| 0,18 | 0,5868 | 0,3443 | 1,044 | 2,00 | 1,5994 | 2,55 | 1,340 |
| 0,20 | 0,6170 | 0,3807 | 1,048 | 2,2 | 1,6432 | 2,70 | 1,357 |
| 0,22 | 0,6455 | 0,4167 | 1,053 | 2,4 | 1,6852 | 2,84 | 1,375 |
| 0,24 | 0,6726 | 0,4521 | 1,057 | 2,6 | 1,7234 | 2,97 | 1,392 |
| 0,26 | 0,6983 | 0,4877 | 1,062 | 2,8 | 1,7578 | 3,09 | 1,406 |
| 0,28 | 0,7229 | 0,5226 | 1,067 | 3,0 | 1,7887 | 3,20 | 1,420 |
| 0,30 | 0,7465 | 0,5572 | 1,071 | 3,5 | 1,8547 | 3,44 | 1,449 |
| 0,35 | 0,8012 | 0,642 | 1,082 | 4,0 | 1,9081 | 3,64 | 1,472 |
| 0,40 | 0,8516 | 0,726 | 1,093 | 4,5 | 1,9519 | 3,81 | 1,489 |
| 0,45 | 0,8978 | 0,806 | 1,103 | 5,0 | 1,9898 | 3,96 | 1,504 |
| 0,50 | 0,9408 | 0,888 | 1,114 | 5,5 | 2,0224 | 4,09 | 1,516 |
Теплофизические свойства стали, представленные в табл. 8, принимаем по справочнику [1].
Таблица 8
Теплофизические свойства стали
| Параметр | 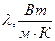
| 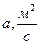
| 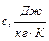
| 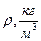
|
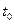 [20°C] [20°C]
| 50,5 | 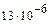
| ||
 [1100°C] [1100°C]
| 28,6 | 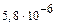
| ||
| Средние значения | 39,6 | 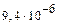
|
Далее в расчетах используются средние значения теплофизических свойств.
Расчет времени нагрева до заданной конечной температуры (1100°C):
Определяем число Био по формуле (111):
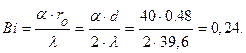
Безразмерная конечная температура определяется по выражению (74):
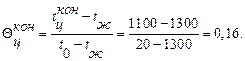
По найденным 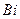 и
и 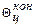 найдем число
найдем число 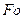 по номограмме (см. рис. 4 прил. 5).
по номограмме (см. рис. 4 прил. 5).
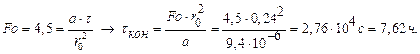
Для определение температуры на оси и поверхности для различных моментов времени выбираем значения чисел 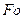 в интервале от 0,25 до
в интервале от 0,25 до 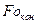 и по номограммам (см. рис. 3, 4 прил. 5) при
и по номограммам (см. рис. 3, 4 прил. 5) при 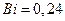 определяем безразмерные температуры центра и поверхности пластины. Данные, полученные по диаграммам, и результаты расчетов сведены в табл. 9.
определяем безразмерные температуры центра и поверхности пластины. Данные, полученные по диаграммам, и результаты расчетов сведены в табл. 9.
Таблица 9
Результаты расчета нагревания термически массивного тела
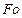
| 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | ||||
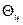
| 0,85 | 0,65 | 0,55 | 0,45 | 0,35 | 0,28 | 0,23 | 0,18 | 0,16 |
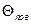
| 0,7 | 0,56 | 0,45 | 0,36 | 0,28 | 0,23 | 0,18 | 0,14 | 0,12 |
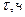
| 0,84 | 1,7 | 2,5 | 3,39 | 4,2 | 5,1 | 5,9 | 6,78 | 7,62 |

| |||||||||
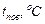
|
Пересчет безразмерных температур в размерные производится с помощью выражения (74).
Расчет распределения температур по сечению цилиндра выполняем с помощью аналитических формул. Безразмерная температура длинного цилиндра при нагревании в среде с постоянной температурой выражается уравнением (114)
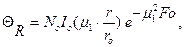
где 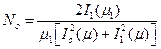 - безразмерный коэффициент;
- безразмерный коэффициент;
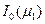 и
и 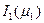 - функции Бесселя первого рода нулевого и
- функции Бесселя первого рода нулевого и
первого порядка.
Для данного случая, при 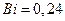 , из табл. 7 находим
, из табл. 7 находим 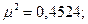
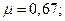
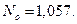 Следовательно, при
Следовательно, при 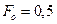 время нагрева
время нагрева 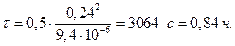 Тогда значение безразмерной температуры на оси цилиндра (
Тогда значение безразмерной температуры на оси цилиндра ( 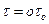 ) составит
) составит
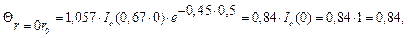
а значение температуры для этой координаты
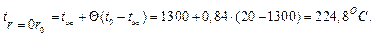
Для остальных значений безразмерной координаты расчет производится аналогично.
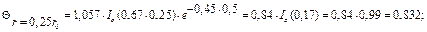
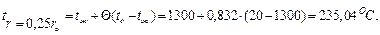
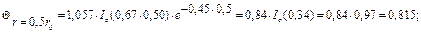
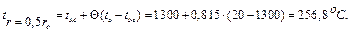
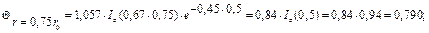
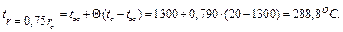
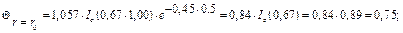
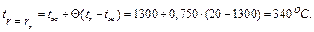
Для других значений чисел 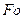 расчет производится аналогично. Итоговые результаты расчета сведены в табл. 10.
расчет производится аналогично. Итоговые результаты расчета сведены в табл. 10.
Таблица 10
Результаты расчетов
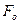
| 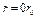
| 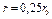
| 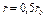
| 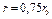
| 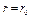
|
| 0,5 | 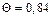 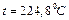
| 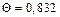 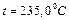
| 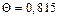 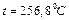
| 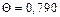 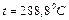
| 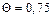 
|

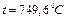
| 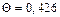
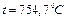
| 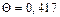

| 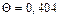
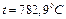
| 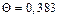

| |
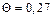
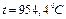
| 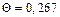
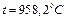
| 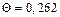
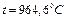
| 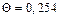

| 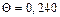
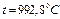
| |
| 4,5 | 

| 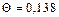
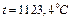
| 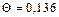
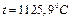
| 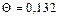
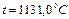
| 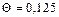
|

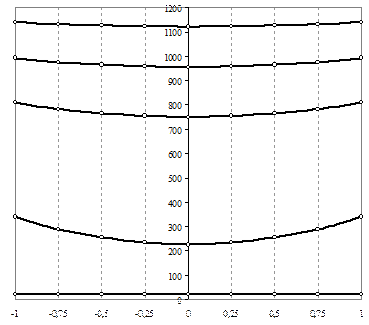
Безразмерная координата
Рис. 7. Графики распределения температуры по тощине заготовки
Дата добавления: 2015-02-13; просмотров: 1823;
