Нагрев массивного тела при граничных условиях III рода
Все тела в зависимости от их способности проводить теплоту делятся на термически тонкие и термически массивные. При l®¥ все тела независимо от формы и размера способны нагреваться (и охлаждаться) так, что перепад температур по сечению отсутствует. Однако у реальных тел значения коэффициента l<<¥ (серебро и медь имеют высокие значения l, но они не превышают 400). Кроме коэффициента теплопроводности материала l условия однозначности учитывают размеры тела, а именно прогреваемую толщину тела d (для пластины d - половина ее толщины, для цилиндра и шара d - радиус, для тел сложной формы d - половина наибольшего линейного размера).
Отношение 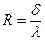 называют внутренним термическим или тепловым сопротивлением тела.
называют внутренним термическим или тепловым сопротивлением тела.
К тонким относятся тела с малым термическим сопротивлением (в пределе d/l®0), к массивным - тела с относительно большим термическим сопротивлением (в пределе d/l®¥).
У тонкого тела термическое сопротивление переносу теплоты теплопроводностью от его поверхности к середине (внутреннее) d/l значительно меньше термического сопротивления теплоотдачи 1/a (внешнего), т.е. 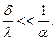
Изменение температуры во времени на поверхности и в середине бесконечной пластины при граничных условиях III рода для идеально тонких и идеально массивных тел при двухстороннем нагреве представлено на рис. 4.
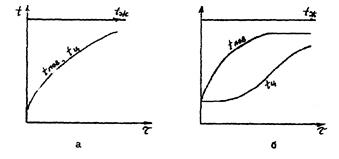
Рис. 4. Изменение температуры поверхности и середины
пластины тонких (а) и массивных (б) тел
Отношение термического сопротивления тела переносу теплоты теплoпpoвoднocтью к термическому сопротивлению теплоотдачи представляет собой число подобия Био
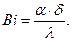 (111)
(111)
Следовательно, для термически тонкого тела Bi®0, для термически массивного тела Bi®¥.
На рис. 5 показано распределение температуры по толщине бесконечной пластины в различные периоды времени нагрева.
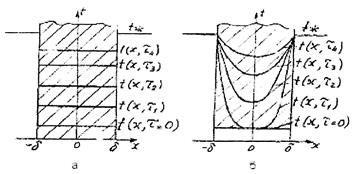
Рис. 5. Распределение температуры по толщине пластины
при Bi®0 (а) и при Bi®¥ (б)
Наиболее распространенным является случай, когда 0,1<Bi<100.
Изменение температуры на поверхности и в середине пластины во времени и распределение ее по толщине пластины для этих условий представлено на рис. 6.
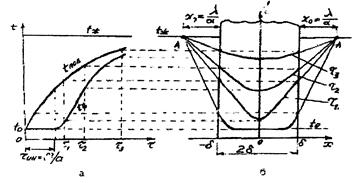
Рис. 6. Изменение температуры пластины во времени (а) и распределение температуры по толщине (б) в условиях, когда Bi конечная величина
В любой период времени нагрева (t >0) касательные к кривой распределения температуры на границе пластины выходят из одной точки А, расположенной на расстоянии 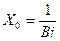 от поверхности пластины (в безразмерных переменных). Учитывая, что
от поверхности пластины (в безразмерных переменных). Учитывая, что 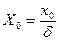 , получим
, получим 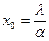 (в размерных переменных).
(в размерных переменных).
Из опыта работы нагревательных устройств установлено, что к тонким телам можно отнести такие, у которых Bi<0,25, а при Bi³0,25 тела следует считать массивными.
Расчет процесса нагревания массивного тела 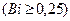 производится аналитическим или графическим методом. Аналитичес-кое решение дифференциального уравнения теплопроводности (44) с граничными условиями третьего рода (50) для тела в форме неограниченной пластины (для
производится аналитическим или графическим методом. Аналитичес-кое решение дифференциального уравнения теплопроводности (44) с граничными условиями третьего рода (50) для тела в форме неограниченной пластины (для 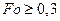 ) имеет вид
) имеет вид
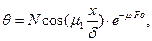 (112)
(112)
где 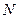 - безразмерный коэффициент;
- безразмерный коэффициент;
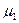 - корень характеристического уравнения.
- корень характеристического уравнения.
Значения 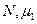 и
и  в зависимости от числа Био берутся из табл. 6. Коэффициент
в зависимости от числа Био берутся из табл. 6. Коэффициент 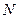 может быть определен также по выражению
может быть определен также по выражению
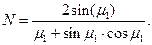 (113)
(113)
Для тела в форме неограниченного цилиндра (для 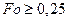 ) при аналитическом методе расчета используется выражение
) при аналитическом методе расчета используется выражение
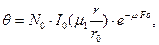 (114)
(114)
где 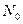 - безразмерный коэффициент;
- безразмерный коэффициент;
 - радиус цилиндра;
- радиус цилиндра;
 - функция Бесселя первого рода нулевого порядка.
- функция Бесселя первого рода нулевого порядка.
Коэффициенты 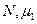 и
и  в зависимости от числа Био берутся из табл. 7. Коэффициент
в зависимости от числа Био берутся из табл. 7. Коэффициент 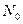 может быть рассчитан по выражению
может быть рассчитан по выражению
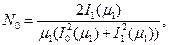 (115)
(115)
где 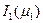 - функция Бесселя первого рода первого порядка.
- функция Бесселя первого рода первого порядка.
Значения функции Бесселя первого рода нулевого и первого порядка приведены в прил. 6.
Графический метод расчета нагревания тела заключается в том, что по заданным значениям чисел 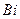 и
и 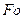 по номограммам, приведенным в прил. 5 на рис. 1 и 2 (для тела в форме пластины) или на рис. 3 и 4 (для тела в форме цилиндра), определяется безразмерная температура
по номограммам, приведенным в прил. 5 на рис. 1 и 2 (для тела в форме пластины) или на рис. 3 и 4 (для тела в форме цилиндра), определяется безразмерная температура 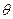 для поверхности и осевой плоскости тела.
для поверхности и осевой плоскости тела.
При построении номограммы использованы аналитические зависимости (112) и (113) между числами подобия. Действительное значение температуры определяется из выражения (74):
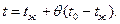
Дата добавления: 2015-02-13; просмотров: 2434;
