Теплообмена
Согласно теории подобия, из физических величин, входящих в дифференциальные уравнения и условия однозначности, можно составить безразмерные комплексы, которые для подобных физических систем одинаковы (1 теорема подобия). Такие комплексы называются числами подобия и имеют определенный физический смысл.
Из рассмотрения уравнений (43)-(47) можно получить следующие числа подобия:
Gr - число подобия Грасгофа, характеризующее отношение подъемных сил к силам вязкости.
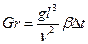 , (57)
, (57)
где 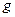 - ускорение силы тяжести, g = 9,81 м/с2;
- ускорение силы тяжести, g = 9,81 м/с2;
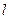 - определяющий размер, м;
- определяющий размер, м;
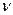 - коэффициент кинематической вязкости среды на границе
- коэффициент кинематической вязкости среды на границе
раздела с твердой поверхностью, м2/с;
b - коэффициент объемного расширения, град-1;
для газов b = 1/Tж = 1/(273 + tж);
Dt = (tс–tж) – разность температур стенки и окружающей среды,
град.
Re - число подобия Рейнольдса, характеризующее соотношение
сил инерции и сил трения (вязкости) в потоке;
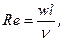 (58)
(58)
где 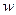 - средняя по сечению скорость потока, м/с;
- средняя по сечению скорость потока, м/с;
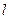 – определяющий размер, м (если поток движется внутри трубы,
– определяющий размер, м (если поток движется внутри трубы,
то 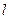 = d).
= d).
Pr - число подобия Прандтля, характеризующее соотношение инерционных свойств среды (гидромеханических) и тепловых.
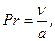 (59)
(59)
где 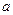 - коэффициент температуропроводности, м2/с.
- коэффициент температуропроводности, м2/с.
Nu - число подобия Нуссельта, характеризующее теплообмен в
пограничном слое газа (жидкости), примыкающем к стенке.
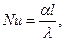 (60)
(60)
где a - коэффициент теплоотдачи конвекцией, Вт/(м град);
l - коэффициент теплопроводности газа (жидкости), Вт/(м2 град);
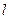 - определяющий размер, м (если газ движется внутри трубы,
- определяющий размер, м (если газ движется внутри трубы,
то 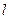 = d).
= d).
В задачах конвективного теплообмена число Нуссельта является искомой величиной, так как в него входит определяемая величина - коэффициент теплоотдачи a. Следовательно, физический смысл числа Nu - безразмерный коэффициент теплоотдачи.
Нестационарный тепловой режим характеризует число подобия Фурье 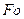 . Это число характеризует безразмерное время процесса нагревания (охлаждения).
. Это число характеризует безразмерное время процесса нагревания (охлаждения).
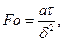 (61)
(61)
где 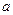 - коэффициент температуропроводности, м2/с.
- коэффициент температуропроводности, м2/с.
t - время нагревания, с;
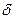 - определяющий размер (для пластины при двухстороннем
- определяющий размер (для пластины при двухстороннем
нагреве - ее полутолщина), м;
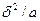 - это отношение характеризует так называемое инерци-
- это отношение характеризует так называемое инерци-
онное время, т.е. время, на которое отстает начало
процесса нагрева середины пластины по сравнению с
началом процесса нагрева поверхности.
При нестационарной теплопроводности большое значение имеет число подобия Био (Bi), имеющее внешнее сходство с числом Нуссельта.
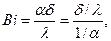 (62)
(62)
где 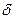 - определяющий размер, м;
- определяющий размер, м;
l – коэффициент теплопроводности твердого тела, Вт/(м·град);
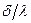 - внутреннее сопротивление стенки, (м2·град)/Вт;
- внутреннее сопротивление стенки, (м2·град)/Вт;
1/a - внешнее сопротивление теплоотдачи, (м2∙град)/Вт.
В отличие от числа Нуссельта, в число Био входит коэффициент теплопроводности твердого тела. Кроме того, в число Био коэффициент теплоотдачи вводится как величина, заданная в условиях однозначности, а в числе Nu рассматривается как искомая величина.
Согласно II теореме подобия, дифференциальное уравнение и его решение можно представить в виде зависимости между числами подобия.
При решении задач конвективного теплообмена такую зависимость можно представить между числом подобия Nu (определяемое число подобия) и числами Gr, Re, Pr, Fo (определяющие числа подобия).
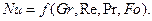 (63)
(63)
Частные уравнения могут иметь более простой вид.
Для стационарного теплового режима при теплообмене поверхности со средой путем свободной конвекции можно пренебречь числами Re и Fo. Зависимость между числами Nu, Gr, Pr описывается следующим выражением:
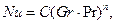 (64)
(64)
где С и n - опытные константы, значения которых можно принимать из табл. 5.
Таблица 5
Значения констант С и n в уравнении Nu = С (Gr·Pr)n
| Режим движения | Gr·Pr | С | n |
| Пленочный | < 10-3 | 0,45 | |
| Переходный от пленочного к ламинарному | 10-3 + 5·102 | 1,18 | 1/8 |
| Ламинарный | 5·102 + 2·107 | 0,54 | 1/4 |
| Турбулентный | > 2·107 | 0,135 | 1/3 |
Все физические параметры выбирают в данном случае по средней температуре пограничного слоя
tп.с = 0,5 (tc + tж). (65)
Физические параметры могут также выбираться по температуре среды tж вдали от поверхности, но тогда будут другие значения С и n, отличающиеся от приведенных в таблице. При выборе расчетных уравнений всегда следует обращать внимание на пределы их применимости.
В качестве определяющего размера для горизонтальных труб берут их наружный диаметр, для вертикальных поверхностей - их высоту, для горизонтальных плоских поверхностей следует брать размер меньшей стороны. При этом, если теплоотдающая поверхность обращена кверху, то полученное по расчету значение a увеличивают на 30%, если теплоотдающая поверхность обращена книзу - уменьшают на 30%.
При стационарном тепловом режиме и вынужденной конвекции можно пренебречь числами Gr и Fo. Зависимость между числами подобия Nu, Re, Pr имеет вид
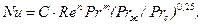 (66)
(66)
где С, n, m - опытные константы.
При вынужденном движении потока внутри трубы при турбулентном режиме (Re>104)
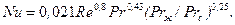 (67)
(67)
При вынужденном движении потока внутри трубы при ламинарном режиме (Re<2,3·103) возможно возникновение свободной конвекции, поэтому в уравнении необходимо учесть число Gr.
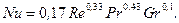 (68)
(68)
Физические свойства принимают по средней температуре потока в трубе.
В качестве определяющего размера принимают внутренний диаметр трубы. В случае некруглого сечения определяется эквивалентный (гидравлический) диаметр
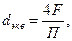 (69)
(69)
где F - площадь поперечного сечения канала, м2;
П - периметр, м.
При вынужденном обтекании потоком плоской поверхности при турбулентном режиме (Re>105)
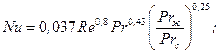 (70)
(70)
при ламинарном режиме (Re<105)
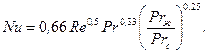 (71)
(71)
Для этих уравнений физические параметры принимаются по температуре потока вдали от поверхности, определяющим размером является длина поверхности пластины.
Во всех уравнениях поправка (Prж/Prc)0,25 учитывается только для капельных жидкостей, для газов (Prж/Prc)0,25 = 1.
Определив значение числа Nu по одной из приведенных формул, легко вычислить коэффициент теплоотдачи конвекцией a, используя выражение (60):
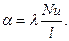 (72)
(72)
При решении задач нестационарной теплопроводности используется зависимость между безразмерной температурой q и числами подобия Bi, Fo.
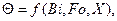 (73)
(73)
где 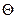 - безразмерная температура в некоторой точке тела,
- безразмерная температура в некоторой точке тела,
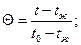 (74)
(74)
t - температура в данной точке тела, °С;
t0 - начальная температура тела перед процессом нагрева
(охлаждения), °С;
tж - температура окружающей среды, °С;
X - безразмерная координата точки, в которой определяется температура t ( 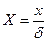 ).
).
Для определения безразмерной температуры используют номограммы (рис. 1-4 прил. 5).
Дата добавления: 2015-02-13; просмотров: 1970;
