Условия однозначности

В самом общем виде процесс переноса теплоты теплопро-водностью и конвекцией описывается уравнением Фурье-Кирхгофа, которое для одномерного движения имеет вид:

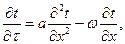(43)

где 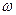- скорость движения потока жидкости вдоль оси X, м/с.

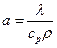- коэффициент температуропроводности, м²/с.

Коэффициент температуропроводности характеризует скорость изменения температуры внутри тела (среды), т.е. меру его инерционности и определяет способность среды проводить теплоту теплопроводностью.

Процесс теплопроводности внутри твердого тела без внутренних источников теплоты в одномерном случае (плоская бесконечная стенка) описывается уравнением ( 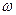=0).

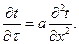(44)

При конвективном теплообмене (конвекция совместно с теплопроводностью) кроме уравнения Фурье-Кирхгофа рассматриваются также дифференциальные уравнения Навье-Стокса, уравнение сплошности и уравнение теплообмена на границе раздела.

Уравнение Навье-Стокса для одномерного движения газа (вдоль оси Х):

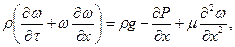(45)

где r - плотность, кг/м³;

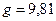м/с² - ускорение сил тяжести;

Р - давление, H/м² (Па);

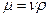- коэффициент динамической вязкости, Па·с (Н·с/м²);

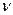- коэффициент кинематической вязкости, м²/с.

Все слагаемые уравнения имеет размерность силы, отнесенной к единице объема. Левая часть уравнения характеризует инерционные силы (в скобках - ускорение элементарной массы газа).

В правой части первый член характеризует силы тяжести, второй - силы давления и третий - силы вязкости. Эти три составляющие определяют сумму сил, действующих на элементарный объем газа.

Уравнение сплошности (выражает принцип постоянства массового расхода газа):

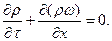(46)

Уравнение на границе теплообмена:

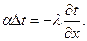(47)

Для получения конкретного решения уравнений (43) - (47) необходимо задать условия однозначности или краевые условия. Условия однозначности включают:

1. геометрические условия, которые дают сведения о форме и размерах тела;

2. физические условия, включающие такие свойства, как теплопроводность l, теплоемкость c_p, плотность r, температуропроводность 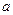, вязкость n и др.;

3. начальные условия, которые характеризуют распределение температуры в теле (среде) в начале процесса; при стационарном тепловом режиме начальные условия не задаются;

4. граничные условия, которые дают сведения об условиях теплообмена на поверхности тела (на границе между окружающей средой и поверхностью).

Граничные условия бывают четырёх родов и задаются соответственно способу нагревания или охлаждения тела.

Граничные условия первого рода характеризуются заданием температуры поверхности тела как функции времени и координат:

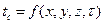, в частном случае 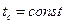. (48)

Граничные условия второго рода характеризуются заданием теплового потока, поступающего на поверхность тела, как функции времени и координат:

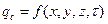, в частном случае 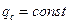. (49)

При граничных условиях третьего рода задается зависимость плотности теплового потока вследствие теплопроводности со стороны тела от температур поверхности тела 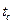и окружающей среды.

В общем виде граничные условия третьего рода задаются как

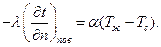(50)

Если теплота на поверхность тела передается конвекцией, то тепловой поток определяется по уравнению (39), а если излучением – по уравнению (41).

Возможен случай передачи теплоты одновременно излучением и конвекцией

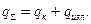(51)

Используя уравнения (39) и (41), его можно записать в следующем виде:

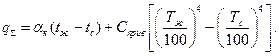(53)

Разделив и умножив оба члена уравнения на разность температур 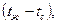после преобразований получим:

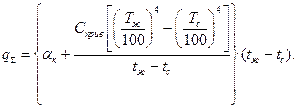(54)

Из формулы (54) следует, что суммарный коэффициент теплоотдачи при переносе теплоты конвекцией и излучением составит

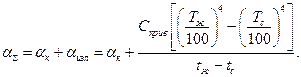(55)

При граничных условиях четвертого рода два тела находятся в плотном контакте между собой. Передача теплоты осуществляется теплопроводностью. В этом случае выполняется равенство температур на границе и тепловых потоков по обе стороны от границы раздела:

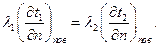(56)

Дифференциальные уравнения (43) или (44) с заданными условиями однозначности дают полную математическую формулировку краевой задачи теплопроводности. Решение задачи осуществляется аналитическими, численными и экспериментальными методами с привлечением теории подобия и моделирования.