Виды сопротивлений

В зависимости от характера внешней нагрузки и от особенностей нагружаемого тела, в поперечных сечениях могут возникать не все шесть внутренних силовых факторов, а какой-либо один или некоторая их комбинация. В соответствии с этим различают следующие виды сопротивлений:

Растяжение (или сжатие) – это вид сопротивления, при котором во всех поперечных сечениях возникает только продольная сила Nz.

Кручение – это вид сопротивления, при котором во всех поперечных сечениях возникает только крутящий момент M_кр.

Чистый изгиб – это вид сопротивления, при котором во всех поперечных сечениях возникает только изгибающий момент M_x (или M_y). Чаще всего изгибающий момент M_x сопровождается наличием поперечной силы Q_y(или момент M_y сопровождается наличием поперечной силы Q_x). В этом случае имеет место поперечный изгиб.

Возможны случаи, когда в поперечных сечениях возникают два и более внутренних силовых фактора одновременно (исключая их комбинации, рассмотренные выше), тогда говорят о сложном сопротивлении.

Все перечисленные виды сопротивлений будут подробно рассмотрены в дальнейших разделах курса.

2.1.7. Напряжения и деформации

Напряжение – это числовая мера интенсивности внутренних сил.

Если известно, что внутренние силы распределяются по сечению напряженного тела равномерно, то в этом случае (рис.2.8):

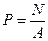, (2.1)

P- напряжение (внутреннее), Па

N – суммарная сила упругости, Н

A- площадь сечения, мм²

В общем случае напряжение P на данной площадке dA будет составлять с этой площадкой некоторый угол α.

Нормальное напряжение 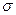направленно перпендикулярно к площадке, а касательное 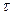по касательной к сечению.

Рис.2.8. Внутренниенапряжения

Рассечем брус, находящийся под действием внешних сил, на две части поперечным сечением, отбросим правую часть и приложим для равновесия внутренние силы (рис.2.9).

Рис.2.9. Схема бруса.

Равнодействующая сила упругости будет действовать по оси бруса и по величине равна N.

Воспользуемся гипотезой плоских сечений: в рассматриваем брусе, все плоские сечения нормальные к оси бруса остаются, и после деформации плоскими и нормальными к оси. Поэтому напряжение во всех точках поперечного сечения будет определяться по формуле:

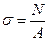. (2.2)

Наличие нормального напряжения σ в любой точке поперечного сечения обусловлено возникновением в этом сечении нормальной силы N или изгибающих моментов М_x и М_y. Наличие касательных напряжений τ обусловлено внутренними силовыми факторами, возникающими в плоскости сечения, т.е. поперечными силами Q_x и Q_y или крутящим моментом.

При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.

Отнесем недеформированное тело к декартовой системе координат Oxyz (рис. 2.10). Положение некоторой точки М в этой системе координат определяется радиус-вектором r (х, у, z). В деформированном состоянии точка М займет новое положение М^/, характеризуемое радиус-вектором r' (х, у, z). Вектор u=r'—r называется вектором полных перемещений точки М. Проекции вектора u на координатные оси определяют компоненты вектора перемещений и (х, у, z), v (х, у, z), w (х, у, z).

Перемещение, при котором взаимное расположение точек тела не меняется, не сопровождается деформациями. В этом случае говорят, что тело перемещается как жесткое целое (линейное перемещение в пространстве или поворот относительно некоторой точки). С другой стороны, деформация, связанная с изменением формы тела и его объема, невозможна без перемещения его точек.

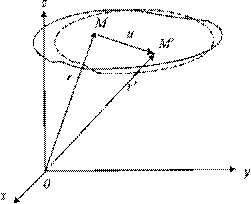
Рис.2.10 Композиция вектора перемещения