Решение. 1. Определяем внешние скручивающие моменты:

1. Определяем внешние скручивающие моменты:

М₀ = 10³ Р_о/ω = 10³ 90/75 = 1200 Н·м

М₁ = 10³ Р₁/ω = 10³ 50/75 = 666,7 Н·м

М₂ = 10³ Р₂/ω = 10³ 20/75 = 266,7 Н·м

М₃ = 10³ Р₃/ω = 10³ 20/75 = 266,7 Н·м

2. Разбиваем вал на характерные участки (рис. 2.27.).

Их границами являются сечения, в которых приложены внешние крутящие моменты М на каждом участке вала. Для этого воспользуемся методом сечений:

1-1: М_к1 = - М₁ = - 666,7 Н·м

2-2: М_к2 = - М₁+ М₀ = - 666,7 + 1200 = 533,3 Н·м

3-3: М_к3= - М₁+ М₀ – М₂ = 266,6 Н·м

Строим эпюру крутящих моментов.

3. Определяем диаметры на каждом участке вала, если из условия прочности:

d = .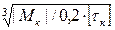

I: d₁ = 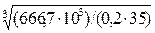= = 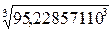45,6 мм.

Принимаем d₁ = 50 мм.

II: d₂ = 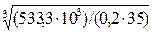= = 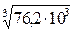42,3 мм.

Принимаем d₂ = 45 мм.

III: d₃ = 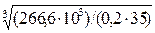= = 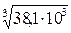33,6 мм.

Принимаем d₃ = 35 мм.

На участке IV диаметр вала принимаем конструктивно d₄ =20 мм. Вычерчиваем эскиз вала в соответствии с принятыми значениями диаметров ступеней.

4. Для определения углов закручивания вала предварительно вычисляем полярные моменты инерции (I_р, м⁴) отдельных сечений вала.

I_pl = π d₁⁴/32 = 3,14·(5,0·10^-2)⁴/32 = 61,3·10^-8 м⁴

I_p2 = π d₂⁴/32 = 3,14· (4,5·10^-2)⁴/32 = 40,2·10^-8 м⁴

I_p3 = π d₃⁴/32 = 3,14· (3,0·10^-2)⁴/32 = 7,9 ·10^-8 м⁴

5. Относительные углы закручивания (φ, град/м) на отдельных участках вала:

φ = М_к / G · I_p.

φ₁ = М_к1 / G · I_p1 = 666,7/8·10¹⁰·61,3·10^-8 = 666,7·10^-2/490,4 = 0,013 рад/м.

|φ₁| < [φ].

φ₂ = М_к2 / G · I_p2 = 533,3/8·10¹⁰·40,2·10^-8 = 533,3·10^-2/321,6 = 0,017 рад/м.

|φ₂| < [φ].

φ₃ = М_к3 / G · I_p3 = 266,6/8·10¹⁰·7,9·10^-8 = 266,6·10^-2/63,2 = 0,042 рад/м.

|φ₂| > [φ].

Следовательно на участке 3-3 жесткость вала не обеспечена.

Вычислим диаметр вала на участке 3-3 из условий жесткости, определив предварительно для этого значение полярного момента инерции I_p3.

I_p3 = М_к3/G·[φ] = 266,6/8·10¹⁰·0,02 = 266,6/0,16·10¹⁰ = 16,67·10^-8 м⁴

d₃ = 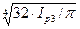= =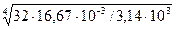36,1 мм

Принимаем d₃ = 40 мм.

Изгиб

2.5.1. Общие сведения

При изгибе характерно: а) у рассматриваемого бруса имеется хотя бы одна плоскость симметрии, б) плоскость действия всех нагрузок (включая реакции опор) совпадает с плоскостью симметрии бруса (рис.2.28). Брус, работающий на изгиб называется балкой. При изгибе в балке существует нейтральная линия – это слой волокон, которые не изменяют своей первоначальной длины – нейтральный слой (рис.2.29).

Рис. 2.28. Схема бруса

Рис.2.29. Изгиб балки

2.5.2. Понятие об изгибающем моменте и поперечной силе

К балке приложены две равные и противоположно направленные по знаку силы (М) (рис.2.30). Рассматривая равновесие, части балки, приложенной слева или справа от сечения n-n, видим, что во всех поперечных сечениях возникает только изгибающий момент, при этом М_и = М – это случай чистого изгиба.

Рис. 2.30.Изгибающий момент

m – приложенный активный момент (внешняя нагрузка); М_и – изгибающий момент.

К балке приложены активные и реактивные силы перпендикулярные к ее оси (рис.2.31). Рассмотрим равновесие частей балки расположенных справа и слева от поперечного сечения. В них действует изгибающий момент и поперечные силы, следовательно, в рассматриваемом случае в точках поперечного сечения действует два вида напряжений:

· Нормальное напряжение – вызывает изгибающий момент.

· Касательное напряжение – соответствует поперечной силе, то есть Q.

В данном случае поперечная сила Q является равнодействующей, внутренних касательных сил в поперечных сечениях и имеет противоположное направление для левой и правой частей балки. Изгибающий момент в сечение балки, численно равен алгебраической сумме моментов относительно центра тяжести сечения. Поперечные силы в сечение балки численно равны алгебраической сумме всех внешних сил действующих справа (слева) от сечения.

Рис. 2.31. Изгибающий момент и поперечная сила

2.5.3. Правило знаков

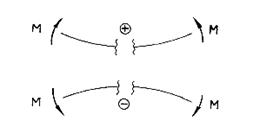
Рис . 2.32.Правило знаков для момента

Если внешняя нагрузка стремиться изогнуть балку выпуклостью вниз, то - знак плюс, и наоборот, если выпуклостью вверх то - знак минус (рис. 2.32).

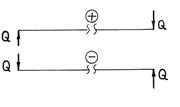
Рис. 2.33.Правило знаков для поперечной силы

Считаем поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной – в противном случае (рис. 2.33).

2.5.4. Эпюры поперечных сил и изгибающих моментов

Для наглядного распределения вдоль оси балки поперечных сил и изгибающих моментов строят соответствующие эпюры. Они дают возможность:

· Определить наличие опасных сечений по длине балки.

· Установить значения поперечных сил и изгибающих моментов в этих опасных сечениях.

При построении эпюр Q и М рекомендуется придерживаться такой последовательности:

1) Найти опорные реакции (для консольной балки их можно не находить)

2) Разбить брус на характерные участки.

3) Применяя метод сечений построить эпюру поперечных сил. Если поперечная сила, изменяясь непрерывно, проходит через нулевое значение, то необходимо определить абсциссу сечения, где Q обращается в ноль.

4) Вычислить в характерных сечениях значения изгибающих моментов и по найденным ординатам построить эпюру М.

2.5.5. Осевой момент инерции

Известно, что при изгибе во всех точках поперечного сечения балки возникают напряжения. В общем случае это нормальное и касательное напряжения. При чистом изгибе только нормальное напряжение, оно зависит от нагрузки и геометрии сечения.

Рис. 2.34. Нейтральная ось.

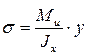, (2.25)

где 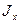-осевой момент инерции;

у – расстояние от рассматриваемого слоя до нейтральной оси (рис. 2.34).

В этой формуле при М_и и 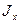величина у переменная, поэтому нормальное напряжение по сечению линейно зависит от расстояния у.

Осевые моменты инерции простейших сечений (рис. 2.35):

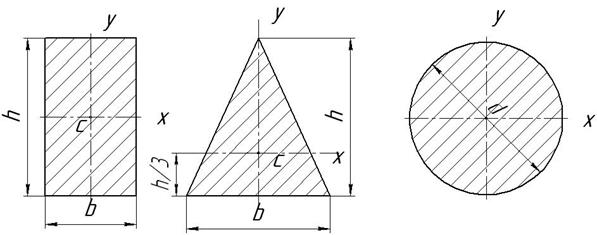
Рис. 2.35. Осевые моменты инерции

1) Прямоугольник

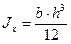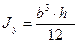; ; (2.26)

2) Треугольник равнобедренный

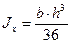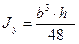, ; (2.27)

3) Круг

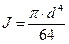. (2.28)

Условие прочности при изгибе по нормальному напряжению:

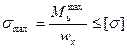(2.29)

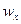- осевой момент сопротивления.

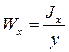, [м³] (2.30)

При решении трех задач выполняется три вида расчетов:

· Проверка прочности балок по нормальным напряжениям (проверочный расчет).

· Подбор поперечного сечения балки (проектный расчет).

· Определение максимальной нагрузки на балку.

2.5.6. Линейные и угловые перемещения при изгибе.

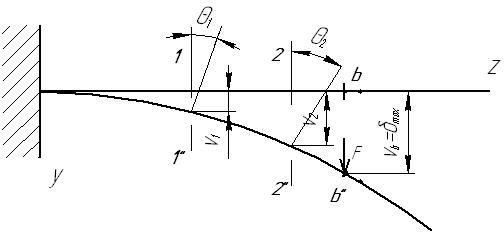
Рис. 2.36.Схема линейных и угловых перемещений при изгибе

При изгибе под действием поперечных нагрузок продольная ось бруса (балки) искривляется. Если изгиб протекает в пределах упругих свойств материала, т.е. в пределах закона Гука, то после снятия нагрузок ось бруса снова выпрямляется. Поэтому изогнутую ось бруса называют упругой линией. По форме, которую при нагружении бруса принимает его упругая линия, можно судить об угловых и линейных перемещениях при изгибе.

Изобразим продольную ось балки, защемленной одним концом. Под действием нагрузки F, перпендикулярной оси балки и расположенной в главной плоскости, ось, оставаясь в этой плоскости изгибается и принимает вид отрезка кривой (рис. 2.36).

При этом центры тяжести произвольных сечений 1 и 2 при изгибе балки переместились соответственно на расстояния v₁ и v₂, а сами сечения, оставаясь плоскими (по гипотезе плоских сечений), повернулись на углы θ₁ и θ₂, которые равны углу между касательной к изогнутой оси в данной точке и направлением оси недеформированного бруса.

Линейные перемещения центров тяжести произвольных поперечных сечений при изгибе называются прогибами бруса, а наибольший прогиб называется стрелой прогиба.

Угол поворота определяется по формуле:

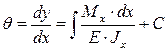, (2.31)

Прогиб по формуле:

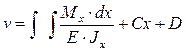. (2.32)

Решения по данным уравнениям очень громоздки, поэтому чаще используют более рациональный способ определения прогиба с помощью интеграла Мора:

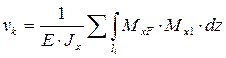, (2.33)

где M_xF – уравнение изгибающего момента от нагрузки F, M_x1 - уравнение изгибающего момента от единичной силы.

Угол поворота определяется по аналогичной формуле, только в этом случае M_x1 – уравнение изгибающего момента от единичного момента.

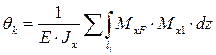(2.34)

Расчет балок на жесткость:

Многие элементы строительных и машиностроительных конструкций требуют расчета на жесткость. Условие жесткости обычно выражается неравенством:

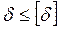, суть, которого в том, что максимальный прогиб не должен превышать допускаемого значения.

Для облегчения расчетов на жесткость приведем формулы прогибов и углов поворота сечений балок в простейших случаях их нагружения (рис.2.37).

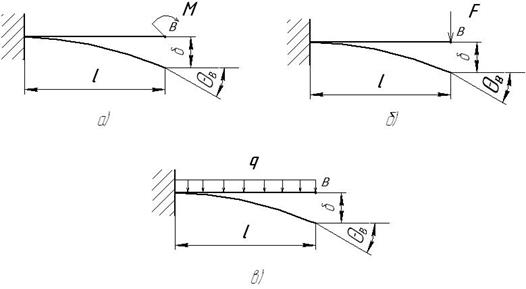
Рис. 2.37. Простейшие случаи нагружения балок

а) 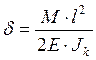, 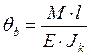(2.35)

б) 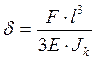, 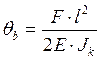(2.36)

в) 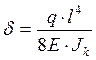, 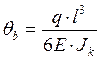(2.37)

2.5.7. Пример расчета балки на изгиб

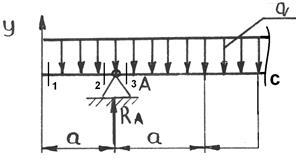
Для заданной балки (рис. 2.38.):

1. Постройте эпюры Q, М_и.

2. Подберите круглое поперечное сечение балки.

Числовые данные варианта взять из приложения 13, схему варианта из приложения 14.

Исходные данные

Схема нагружения и результаты.

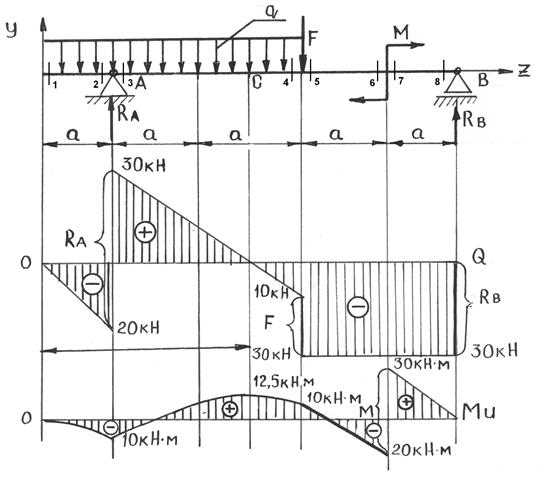
Рис. 2.38. Схема нагружения и эпюры.

1) Определим опорные реакции, для чего составим два уравнения моментов:

Σ М_А=0 q·a·0,5a – q·2a·a – F·2a – M + R_B·4а = 0

20·1·0,5-20·2·1 – 20·2 – 50+4·R_B = 0

Σ М_В=0 q·3a·3,5a – R_A·4a + F·2a – M = 0

20·3·3,5 – R_A·4 + 20·2 – 50 = 0

Откуда R_B = 120/4 = 30 кН

R_A = 200/4 = 50 кH

Для проверки правильности определения опорных реакций составляем сумму проекций всех сил, приложенных к балке на вертикальную ось Y:

Σ F_iy = 0 -q·3а + R_A – F + R_B = 0

-20·3 + 30 – 20 + 50 = 0

2) Намечаем характерные сечения:

К характерным сечениям относятся:

а) сечения, расположенные бесконечно близко по обе стороны от точек приложения сосредоточенных сил и моментов;

б) сечения, расположенные в начале и в конце каждого участка с распределенной нагрузкой;

в) сечения, расположенные бесконечно близко к опорам, а также на свободных концах.

3) Вычисляем значения поперечных сил в характерных сечениях:

Рассматриваем левую отсеченную часть:

1:1 Q_у1=0

М_х1=0

2:2 Q_у2=-q·а=-20·1= -20 кН

М_х2=-q·а·0,5а=-20·0,5= -10 кН

3:3 Q_у3=-q·а+R_Ау=-20·1+50=30 кН

М_х3=-q·а·0,5а=-20·0,5=-10 кН

4:4 Q_у4=-q·3а+R_Ау=-20·3+50=-10 кН

М_х4=-q·3а·1,5а+R_Ау·2а=10 кН

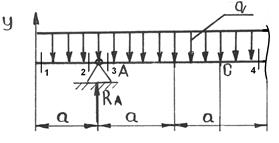
Для сечений 5-8 удобнее рассматривать правую отсеченную часть:

5:5 Q_у5=-R_Ву=-30 кН

М_х5=-М+R_Ву·2а=-50+30·2=10 кН

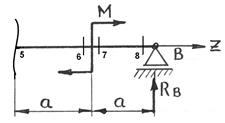
6:6 Q_у6=-R_Ву=-30 кН

М_х6=-М+R_Ву·а=-50+30=-20 кН

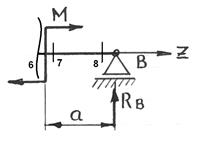
7:7 Q_у7=-R_Ву=-30 кН

М_х7=R_Ву·а=30 кН

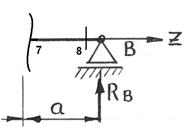
8:8 Q_у8=-R_Ву=-30 кН

М_х8=0

Поперечная сила Q в некоторой точке С принимает нулевое значение Q = 0, поэтому необходимо определить абсциссу «нулевого сечения», для этого необходимо составить уравнение равновесия сил относительно сечения С:

-q·z_c + R_A = 0 z_c = R_A/q = 50/20 = 2,5 м.

с:с М_хс=-q·z_с· z_с /2+ R_Ау(2,5-а)=12,5 кН

Строим эпюру поперечных сил и изгибающих моментов.

4) Определим диаметр круглого поперечного сечения балки:

W_x= |М_иmах| / [σ],

Наибольшее значение по модулю момент имеет в сечении 6 и 7:

|М_иmах| =30 кН·м.

W_x= 30·10³ /160·10⁶ = 0,1875·10^{-3 м.}

d = 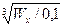= = 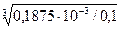0,123 мм.

Правила контроля эпюр Q_у и M_x:

Эпюра Q_y является прямолинейной на всех участках; эпюра M_x – криволинейная (квадратная парабола) на участке под равномерно распределенной нагрузкой, причем, выпуклость кривой всегда обращена навстречу нагрузке q, и прямолинейная на всех остальных участках.

Под точкой приложения сосредоточенной силы (реакции) на эпюре Q_y обязательно должен быть скачок на величину этой силы (реакции). Аналогично, под точкой приложения сосредоточенного момента на эпюре M_x обязателен скачок на величину момента.

Если на участке, под распределенной нагрузкой, эпюра Q_y пересекает ось (Q_y = 0), то эпюра M_x в этом сечении имеет экстремум.

На участках с поперечной силой одного знака эпюра M_x имеет одинаковую монотонность. Так, при Q_y > 0 эпюра M_x возрастает слева направо; при Q_y < 0 – убывает.

Порядок линии на эпюре Qy всегда на единицу меньше, чем на эпюре M_x. Например, если эпюра M_x – квадратная парабола, то эпюра Q_y на этом участке – наклонная прямая; если эпюра M_x – наклонная прямая, то эпюра Q_y на этом участке – прямая, параллельная оси; если M_x = const (прямая, параллельная оси), то на этом участке Q_y = 0.