Растяжение и сжатие
2.2.1. Продольная деформация
Возьмем призматический брус с постоянной площадью поперечного сечения А, и приложенные по бокам две равные и противоположно направленные силы F, направленные по оси бруса (рис.2.11)


Рис.2.11. Продольная и поперечная деформации
Брус в продольном направлении удлиняется, а его поперечные размеры уменьшаются. Удлинение бруса будет равно 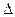 l = l1 – l,
l = l1 – l,
где 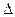 l – полное или абсолютное удлинение.
l – полное или абсолютное удлинение.
Более удобной мерой деформации является относительное удлинение (продольная деформация), определяемая по формуле:
ε = 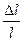 . (2.3)
. (2.3)
2.2.2. Поперечная деформация
Абсолютная поперечная деформация:
D А = А – А1. (2.4)
Относительное изменение площади поперечного сечения (поперечная деформация):
ε 0 = 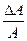 . (2.5)
. (2.5)
Опытами установлено, что даже при небольших деформациях бруса в продольном направлении его поперечные размеры изменяются.
Поперечные деформации при растяжении или сжатии пропорциональны продольной деформации и характеризуются коэффициентом Пуассона. Коэффициент Пуассона при растяжении равен:
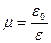 , (2.6)
, (2.6)
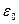 - поперечное относительное сжатие;
- поперечное относительное сжатие; 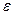 - продольное относительное удлинение.
- продольное относительное удлинение.
При сжатии:
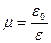 , (2.7)
, (2.7)
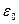 - поперечное относительное растяжение;
- поперечное относительное растяжение; 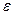 - продольное относительное сжатие.
- продольное относительное сжатие.
Для различных материалов 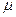 составляет от 0 до 0,5, в практических расчетах для стали принимают
составляет от 0 до 0,5, в практических расчетах для стали принимают 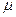 =0,32-0,35.
=0,32-0,35.
2.2.3. Закон Гука
Основной закон сопротивления материалов выражает прямую пропорциональность между нормальным напряжением и продольной деформацией:
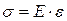 , (2.8)
, (2.8)
где Е – модуль продольной упругости (модуль Юнга), [Па]
(для стали Е = 2ּ105 МПа)
Модуль упругости характеризует жесткость материала, т.е. способность сопротивляться деформациям.
Если в законе Гука расписать продольную деформацию то получим:
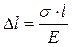 . (2.9)
. (2.9)
2.2.4. Диаграммы растяжения
Механические характеристики устанавливают границу безопасности эксплуатации элементов конструкции при статических и динамических нагрузках. К числу основных характеристик относятся: предельное напряжение, твердость, ударостойкость, вязкость, вес конструкционных материалов.
Материалы можно разделить на хрупкие и пластичные.
Пластичные обладают способностью деформироваться в широких пределах. К ним относятся: алюминиевые, медные, золотые сплавы, малоуглеродные стали. Хрупкий материал разрушается без предварительной деформации. К ним относятся: чугун, высокоуглеродные стали, металлы, керамические сплавы, стекло.
Для выполнения расчетов конструкции на прочность необходимо знать свойства материалов, из которых эти конструкции изготовлены. Наиболее распространенным испытанием материалов является испытание на растяжение. Это объясняется тем, что механические характеристики, получаемые при растяжении, позволяют судить о поведении материала при других деформациях: сжатии, сдвиге, кручении и изгибе.
Рис.2.12. Схема образца
Образец постепенно нагружается силой возрастающей от 0 до величины разрушающей образец (рис.2.12). Величина нагрузки измеряется и записывается в виде кривой зависимости между растягивающей нагрузкой и полученным удлинением.
Рассмотрим диаграмму растяжения малоуглеродистой стали (рис.2.13): в начале испытания (до отметки 1 с ординатой Nпц) удлинение Δl растет пропорционально силе F, тем самым подтверждается закон Гука. Далее удлинение Δl возрастает непропорционально силе F. При некотором значении силы (отметка 2) образец удлиняется без увеличения нагрузки. Это явление называется текучестью металла.
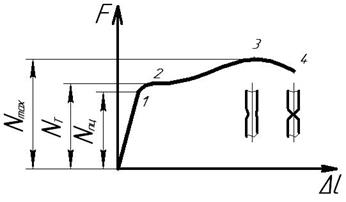
Рис.2.13.Диаграмма растяжения малоуглеродистой стали
По окончании стадии текучести, материал образца снова начинает сопротивляться нагрузке до отметки 3 с ординатой Nmax , после которой наблюдается снижение сопротивляемости образца нагрузке. Это обстоятельство объясняется тем, что на образце начинает появляться местное сужение (шейка) и в дальнейшем диаграмма фиксирует уже растяжение не всего образца, а только его участка в зоне образовавшейся шейки. Момент окончательного разрушения образца обозначается цифрой 4.
Весьма хрупким материалом является чугун. Для образца из обычного серого литейного чугуна относительное остаточное удлинение при разрыве не превышает 0,015%. При разрыве образцов из хрупких материалов шейка не образуется, и растягивающее усилие растет до момента разрушения (рис.2.14).
Деформации чугуна очень малы, они с самого начала не следуют закону Гука, а потому диаграмма получается криволинейной (кривая 1) (рис.2.14 а).
Диаграмма растяжения чугуна (кривая 2) по характеру аналогична диаграмме сжатия, но предел прочности при растяжении значительно ниже, чем предел прочности при сжатии.
Иными словами, чугун значительно хуже работает на растяжение, чем на сжатие. При сжатии чугунный образец разрушается в результате образования наклонных трещин, направленных примерно под углом 45° к оси образца (как это показано на рис.2.14 б), т. е. параллельно площадкам, в которых действуют наибольшие касательные напряжения.
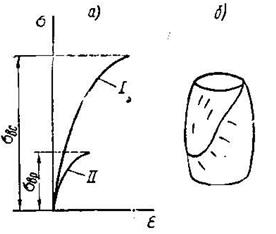
Рис.2.14 Диаграмма растяжения чугуна
Характеристики материала:
1. Отношение растягивающего усилия F1 к площади поперечного сечения А0 – предел пропорциональности.
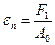 . (2.10)
. (2.10)
2. Отношение растягивающих усилий в точке 2 к первоначальному поперечному сечению стержня – предел упругости.
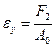 , (2.11)
, (2.11)
где 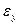 - напряжение при котором величина относительной и остаточной деформации не превышает 0,005%
- напряжение при котором величина относительной и остаточной деформации не превышает 0,005%
3. Отношение растягивающего усилия соответствующего текучести материала к площади первоначального поперечного сечения – предел текучести.
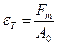 , (2.12)
, (2.12)
где 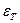 - напряжение, при котором происходит рост деформации без увеличения нагрузки.
- напряжение, при котором происходит рост деформации без увеличения нагрузки.
4. Отношение наибольшего растягивающего усилия F3 к площади первоначального сечения – предел выносливости (прочность).
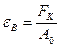 . (2.13)
. (2.13)
2.2.5. Основы прочностных расчетов элементов конструкций
Целью прочностных расчетов является: определить напряжения при фактической нагрузке, а затем сопоставить их с опасным значением.
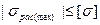 (2.14)
(2.14)
Расчеты на прочность:
1.Отношение предельного напряжения σпр к расчетному σ называется коэффициентом запаса прочности S:
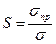 , (2.15)
, (2.15)
Прочность элемента конструкции обеспечивается, если действительный коэффициент запаса прочности не ниже требуемого: 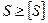
Разделив предельное напряжение на нормативный коэффициент запаса прочности, получим допускаемое напряжение 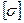 :
:
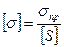 , тогда условие прочности имеет вид:
, тогда условие прочности имеет вид:
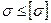 т. е. прочность элемента конструкции обеспечивается если наибольшее напряжение, возникающее в нем, не превышает допускаемого.
т. е. прочность элемента конструкции обеспечивается если наибольшее напряжение, возникающее в нем, не превышает допускаемого.
Условие прочности применительно к расчетам на прочность при растяжении (сжатии) имеет вид:
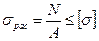 . (2.16)
. (2.16)
Для хрупких материалов допускаемое напряжение растяжения и сжатия получают исходя из предела текучести:
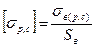 (2.17)
(2.17)
Для пластичных материалов предельным напряжением является предел текучести:
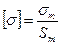 . (2.18)
. (2.18)
2.2.6. Пример расчета стержня на растяжение – сжатие
Двухступенчатый стальной брус, длины ступеней которого указаны на схеме (рис.2.15), нагружен силами F1, F2 и F3. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса l, приняв E=2•10 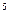 МПа. Произвести оценку прочности по участкам стержня и вычислить запас прочности, если σпр = 200 МПа, σу = 240 МПа. Числовые данные варианта взять из приложения 9, схему варианта из приложения 10.
МПа. Произвести оценку прочности по участкам стержня и вычислить запас прочности, если σпр = 200 МПа, σу = 240 МПа. Числовые данные варианта взять из приложения 9, схему варианта из приложения 10.
Схема нагружения и исходные данные
Fl= 120 кН; F2= 80 кН; F3= 80 кН; A1= 12 см2; A2= 10 см2; A3= 18 см2.
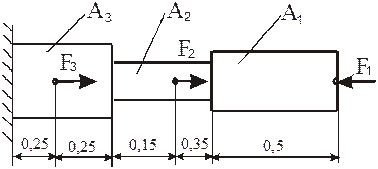
Рис. 2.15. Схема нагружения
Решение
Выделяем характерные участки стержня. Границами участков являются сечения, в которых приложены силы или изменяется площадь поперечного сечения (рис. 16). В нашем примере пять характерных участков.
 |
Рис. 2.16. Схема нагружения с участками
Определяем продольные силы для каждого участка стержня методом сечений
1-1
 ∑Fix=0
∑Fix=0
- N1 – F1 = 0
N1 = - F1
N1 = - 120 кН
Рис. 3.
N1 – отрицательная, следовательно, она направлена в тело стержня.
N1= - 120 кН.
2-2 На участке 2-2 новые силы, не приложены и следовательно N2 = N1 = -120 кН.
 3-3
3-3
∑Fix=0
- F1 + F2 – N3 = 0
N3 = F2 – F1 = 80 – 120 = - 40
N3 = -40 кН
4-4 N4 = -40 кН
 5-5
5-5
∑Fix=0
- F1 + F2 + F3 – N5 = 0
N5 = F2 + F3 – F1= 80 + 80 – 120 = 40
N5 = 40 кН
Строим эпюру продольных сил (рис. 17).
 |
Рис. 2.17. Схема нагружения с эпюрами
Определяем нормальные напряжения в пределах каждого характерного участка стержня:
σ1 = N1/A1 = (-120·103)/(12·102) = -100 МПа < σпр
σ2 = N2/A2 = (-120·103)/(10·102) = -120 МПа < σпр
σ3 = N3/А2 = (-40·103)/(10·102) = -40 МПа < σпр
σ4 = N4/A3 = (-40·103)/(18·102) = -25 МПа < σпр
σ 5 = N5/A3 = (40·103)/(18·102) = 25 МПа < σпр
Строим эпюру нормальных напряжений σ (рис. 2.17.)
Если σ > σ пр, то поперечное сечение стержня увеличивается и площадь его определяется по формуле:
А = N/ σ пр
Определяем коэффициент запаса прочности для второго участка стержня, на котором нормальное напряжение оказалось наибольшим.
S = σу / | σ2| = 240/120 = 2
Определяем абсолютные удлинения каждого характерного участка и подсчитываем перемещения сечений, совпадающих с границами участков:
lА= 0
lВА =lА+ΔlВА = 0 + (N5·l5)/E = 0 + (σ5·l5)/E = (25·0,25·103)/(2·105) = 0,0312 мм
lСА= lВА + ΔlСВ = lВА + (σ4·l4) /Е = 0,0312 – (25·0,25·103)/(2·105) = 0
lда = lСА + ΔlДС = lСА + (бз·lз)/Е = 0 – (40·0,15·103)/(2·105) = - 0,03 мм
lЕА = lДА + (б2×l2)/Е = - 0,03 – (120·0,35·103)/ (2·105) = - 0,24 мм
lКА = lЕА +(б1×l1)/Е = = - 0,24 – (100·0,5·103)/(2·105) = -0,49 мм.
Строим эпюру абсолютных удлинений (рис. 17).
Сдвиг
2.3.1. Чистый сдвиг. Закон Гука при сдвиге
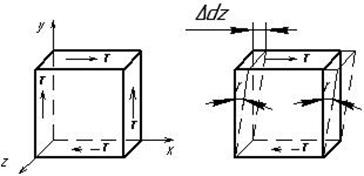
Рис. 2.18. Чистый сдвиг
При чистом сдвиге на четырех гранях выделенного элемента возникают только касательные напряжения, а две грани свободны от напряжений (рис.2.18).
Явление сдвига состоит в том, что под действием внешних сил первоначальная форма выделенного элемента искажается, например, горизонтальные площадки сдвигаются относительно друг друга на расстояние Δdz, называемое абсолютным сдвигом, и угол 90 градусов между смежными площадками изменяется на величину γ. Этот угол называется углом сдвига или угловой деформацией.
Установлено, что касательные напряжения и угол сдвига в пределах упругих деформаций связаны между собой прямой пропорциональной зависимостью:
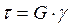 , которая называется законом Гука при сдвиге. Коэффициент пропорциональности G называется модулем сдвига и характеризует жесткость материала при сдвиге.
, которая называется законом Гука при сдвиге. Коэффициент пропорциональности G называется модулем сдвига и характеризует жесткость материала при сдвиге.
Между модулем упругости Е, модулем сдвига G и коэффициентом Пуассона μ существует зависимость:
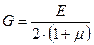 . (2.19)
. (2.19)
2.3.2. Расчет на сдвиг (срез)
Если два бруса соединить между собой штифтом, а затем нагрузить направленными в противоположные сторонами силами F, то при значительных силах или небольшом диаметре штифта, он может быть разрушен по сечению, расположенному в плоскости соприкасания поверхностей соединяемых брусьев. Такое разрушение соединительных деталей (штифта, болта, заклепки, шпонки), происходящее под действием нагрузок, перпендикулярных их собственным осям (поперечные нагрузки), называется срезом(рис.2.19).
Условие прочности при расчете на срез имеет вид:
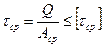 , (2.20)
, (2.20)
где 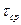 - расчетное напряжение среза в поперечном сечении детали;
- расчетное напряжение среза в поперечном сечении детали; 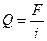 - поперечная сила, возникающая в этом сечении;
- поперечная сила, возникающая в этом сечении; 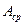 - площадь поперечного сечения срезаемой детали (площадь среза); I - число соединительных деталей.
- площадь поперечного сечения срезаемой детали (площадь среза); I - число соединительных деталей.
При расчете болтов, штифтов, шпонок и прочего принимают: 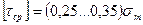 или
или 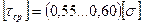
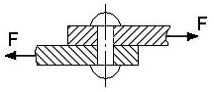
Рис.2.19. Срез
Дата добавления: 2015-02-10; просмотров: 2266;
