Внутренние силы. Метод сечений

Рассмотрим тело произвольной формы в “спокойном”, ненагруженном состоянии. Между его частицами всегда существуют силы взаимодействия, которые стремятся сохранить его как единое целое, то есть препятствуют изменению взаимного расположения частиц. При нагружении тела произвольной внешней нагрузкой силы взаимодействия между частицами изменяются, появляются дополнительные силы взаимодействия, которые приводят к изменению взаимного расположения частиц тела, то есть к его деформации.

Эти дополнительные силы взаимодействия называются внутренними силами упругости (ВСУ) и являются предметом изучения сопротивления материалов.

Анализ характера распределения внутренних сил упругости осуществляется при помощи метода сечений. Это метод, позволяющий выявить внутренние усилия в сечении стержня, перевести их в разряд внешних сил и определить их численные значения.

Рассмотрим тело произвольной формы, нагруженное самоуравновешенной системой сил (рис. 2.6,а). В интересующем нас сечении мысленно рассечем его плоскостью на две части (рис. 2.6,б).

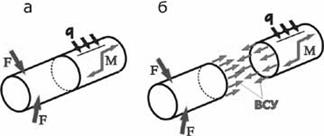
Рис.2.6. Тело, нагруженное самоуравновешенной системой сил

Внутренние силы упругости определяют взаимодействие между частицами тела, расположенными по разные стороны от мысленно проведенного сечения. В разных сечениях тела возникают разные внутренние силы упругости, но по принципу действия и противодействия они всегда взаимны. Правая отсеченная часть тела действует на левую точно так же, как и левая, на правую, а это означает, что равнодействующая внутренних сил может определяться из условий равновесия, как левой отсеченной части тела, так и правой.

Из курса теоретической механики известно, что любую произвольную систему сил можно привести к центру тяжести сечения. В результате внутренние силы упругости, действующие в рассматриваемом сечении, приводятся к главному вектору R и главному моменту M. Выберем прямоугольную систему координат OXYZ так, что ось Z будет направлена по нормали к поперечному сечению, а оси X и Y лежат в плоскости сечения. Проецируя главный вектор R на каждую из осей, а главный момент M на каждую из координатных плоскостей, получим шесть величин: 3 силы и 3 момента, которые называются внутренними силовыми факторами (рис.2.7).

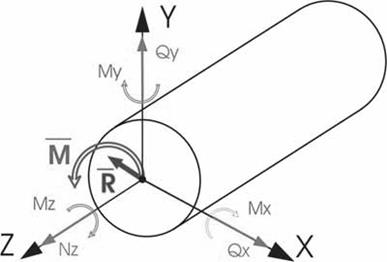
Рис.2.7 Схема внутренних силовых факторов

Полученные таким образом шесть внутренних силовых факторов (ВСФ) имеют строго определенные названия:

N_z – продольная (нормальная) сила;

Q_x, Q_y – поперечные (перерезывающие) силы;

M_x, M_y – изгибающие моменты;

M_z – крутящий момент.

Иногда обозначение M_z заменяют на M_кр или M_к, более точно отвечающие физическому смыслу этой величины.

График, показывающий, как меняется внутренний силовой фактор по длине рассматриваемого тела, называется эпюрой.

Если внешние силы заданы, то внутренние силовые факторы вычисляются на основании условия равновесия, как алгебраические суммы проекций сил и моментов, действующих на мысленно отсеченную часть тела.

Правильность построения эпюры обеспечивается, в первую очередь, надлежащим выбором характерных сечений, то есть тех сечений, в которых величина внутреннего силового фактора обязательно должна быть определена.

К характерным сечениям относятся:

1) сечения, расположенные бесконечно близко по обе стороны от точек приложения сосредоточенных сил и моментов;

2) сечения, расположенные в начале и в конце каждого участка с распределенной нагрузкой;

3) сечения, расположенные бесконечно близко к опорам, а также на свободных концах.