Работа постоянной силы

Так как 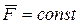,то по свойствам интегрирования:

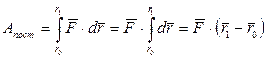. (1.105)

Работа постоянной силы равна скалярному произведению силы на полное перемещение точки приложения силы.

Кроме того, работа постоянной силы не зависит от траектории перемещения точки приложения силы, а определяется только ее начальным и конечным положениями или работа постоянной силы равна скалярному произведению силы на полное перемещение точки приложения силы в направлении действия силы.

Работа силы тяжести

Для определения работы, которую совершает сила тяжести Р, рассмотрим движение тела вниз по наклонной плоскости (рис.1.50).

Рис. 1.50

При скольжении по наклонным плоскостям работа силы тяжести определяется высотой h, на которую опускается груз, и не зависит от угла наклона плоскости.

Проекция NO перемещения s=MN на направление силы тяжести, т. е. на вертикаль, равна высоте h наклонной плоскости. Согласно определению работы:

А= F·s, (1.106)

т. е. работа силы равна проекции перемещения точки ее приложения на направление силы, умноженной на величину силы.

Работа силы тяжести при перемещении тела вдоль наклонной плоскости из точки N в точку М будет равна силе тяжести, умноженной на высоту наклонной плоскости:

A=P·h . (1.107)

Тот же результат получится и для наклонной плоскости NМ₁. Таким образом, работа силы тяжести не зависит от угла наклона, а только от высоты наклонной плоскости; сила тяжести совершила бы такую же работу и в том случае, если бы груз опустился на такое же расстояние прямо по вертикали.

Отсюда можно сделать вывод: по какому бы пути ни опускался груз, сила тяжести Р совершает работу

А = Р·h. (1.108)

где h — высота, на которую опустился груз. Действительно, любой путь можно представить себе состоящим из большого числа участков различных наклонных плоскостей (рис. 1.51). Работа на каждом участке определяется высотой, на которую опустился груз при перемещении по этому участку. Работа же по всему пути равна действующей на груз силе тяжести, умноженной на полную высоту, на которую опустился груз.

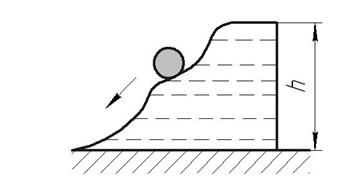
Рис. 1.51

Любой путь можно представить как совокупность большого числа малых участков наклонных плоскостей.

Аналогичный вывод можно сделать и для подъема данного тела по наклонной плоскости или какому-либо другому пути. В этом случае работа против силы тяжести также не будет зависеть от формы пути, а только от высоты поднятия.

1.3.8. Принцип Д’Аламбера

Сила инерции материальной точки – это условная сила, линия действия которой противоположна действительному ускорению точки и равная по величине произведению массы точки на её ускорение:

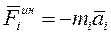, (1.109)

Сила инерции механической системы – это сумма сил инерции всех точек системы:

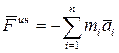. (1.110)

Теорема: Сила инерции механической системы равняется произведению массы всей системы на ускорение её центра масс, взятое с обратным знаком:

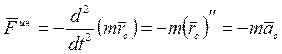, (1.111)

при вращательном движении .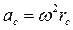

Центр инерции системы – точка приложения силы инерции системы.

Положение центра инерции ищется как точка приложения равнодействующей всех элементарных сил инерции. Следует помнить, что поскольку силы инерции могут вести себя не так, как силы тяжести, то Центр инерции и центр тяжести тела могут не совпадать.

Инерционный момент – это условный момент, который действует относительно оси вращения тела и равен произведению момента инерции тела относительно этой оси на угловое ускорение тела, взятое с противоположным знаком:

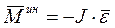, (1.112)

Принцип Д’Аламбера: если к заданным внешним силам, действующим в системе, добавить силы инерции тел и их инерционные моменты, то можно считать, что система находится в равновесии.

Доказательство: в общем случае движение материального тела описывается двумя векторными уравнениями:

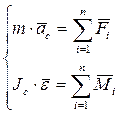, (1.113)

де 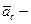ускорение центра масс тела;

J_c – собственный момент инерции тела.

C учетом теоремы о силе инерции механической системы и определения силы инерции (1.111) и инерционного момента (1.112)

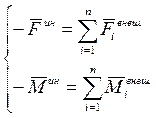, (1.114)

Если собрать все слагаемые в одну часть, то:

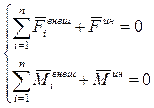, (1.115)

Полученные уравнения совпадают с уравнениями, описывающими равновесное положение тела, хотя тело находится в движении.

1.3.9. Количество движения механической системы

Количество движения материальной точки есть произведение массы точки на ее скорость

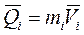. (1.116)

Количество движения механической системы это сумма количеств движения всех точек системы

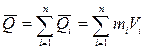. (1.117)

При использовании формулы (1.117), не обязательно разбивать систему только на материальные точки: можно на отдельные тела или группы тел, но внутри этих групп не должно быть относительных смещений.

Теорема: количество движения системы материальных тел равно произведению массы всей системы на скорость ее центра масс:

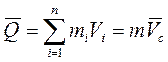, (1.118)

Следствие. Количество движения тела равно произведению массы на скорость его центра масс.

Термин «элементарный» в сочетании с какой-либо характеристикой означает дифференциал этой характеристики.

Термин «сумма элементарных» в сочетании с какой-либо характеристикой означает интеграл этой характеристики.

Элементарный импульс силы – это произведение силы на элементарный промежуток времени действия силы:

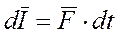, (1.119)

Полный импульс силы – это сумма всех элементарных импульсов в течение времени действия силы:

. (1.120)