Динамика

Динамика изучает движение материальных тел как результат их взаимодействия с другими телами.

Так как мерой взаимодействия является сила, то поведение сил и изменение характеристик движения во времени должны быть взаимосвязаны.

Все задачи динамики можно условно разделить на две категории:

- зная характеристики движения, определить силы, вызвавшие такое движение (прямая задача);

- зная силы, определить характеристики движения (обратная задача).

При рассмотрении статики силы считались постоянными величинами, в динамике будем учитывать, что сила – величина переменная.

1.3.1. Аксиомы динамики

Аксиома №1: сила – это векторная величина.

Следовательно, с силами можно совершать те же операции, что и с векторами, т.е. складывать, вычитать, проецировать, умножать на скаляр или другой вектор и т.д.

Аксиома №2: любое материальное тело можно представить как совокупность конечного числа материальных точек.

Аксиома №3: если силы, действующие на материальную точку, уравновешены или отсутствуют, то эта точка сохраняет состояние покоя или движется равномерно и прямолинейно (по инерции).

Движение равномерное и прямолинейное называется инерционным движением.

Система координат, в которой выполняется первая аксиома, называется инерционной системой отсчета. Не все системы координат являются инерционными, поэтому чтобы пользоваться теоремами и законами динамики, необходимо выбрать систему координат. На практике следует учитывать, что инерционной можно считать только систему координат с центром в центре масс Солнца и осями, направленными на удаленные внегалактические объекты. Систему координат, располагающуюся на поверхности земли, можно считать инерционной условно. При этом погрешность расчетов подавляющего большинства задач о движении тел вблизи поверхности Земли будет достаточно мала.

Аксиома №4: если на материальную точку действует сила, то эта точка будет двигаться с ускорением, прямо пропорциональным этой силе. Коэффициент пропорциональности между силой 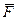и ускорением 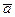называется массой материальной точки m.

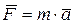. (1.80)

Поскольку в теоретической механике рассматриваются тела, движущиеся со скоростями только гораздо меньше скорости света, то массу можно считать постоянной величиной.

Возьмем две материальные точки с различными массами, например m₁>m₂, и подействуем на каждую из них одной и той же силой 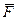. На основании четвертой аксиомы получим:

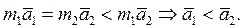(1.81)

Видим, что чем больше масса точки, тем медленнее она будет двигаться под действием одной и той же силы при прочих равных условиях.

Инертность – это способность тел сопротивляться попыткам изменить их состояние.

Масса является мерой инертности поступательного движения тел. Чем больше масса, тем труднее привести тело в движение и труднее, затем остановить его.

Аксиома №5: две материальные точки действуют друг на друга с силами равными по величине, лежащими на одной прямой и направленными в разные стороны (действие равно противодействию).

1.3.2. Уравнения движения точки в декартовой системе координат

Рассмотрим движение материальной точки. Пусть на нее действуют силы 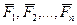. Так как речь идет о материальной точке, то эти силы обязательно будут сходящимися, и их можно заменить равнодействующей:

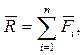(1.82)

где i = от 1 до n.

На основании четвертой аксиомы имеем:

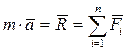(1.83)

Как известно из кинематики, 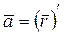, тогда:

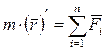(1.84)

Если перейти к проекциям, то получим систему дифференциальных уравнений второго порядка, описывающих поведение материальной точки вдоль каждой из осей координат:

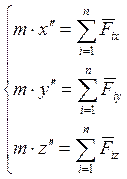. (1.85)

1.3.3. Одномерное движение

Движение точки будет одномерным, если для его описания достаточно одной оси координат, траектория будет прямой линией.

Выбираем систему координат так, чтобы ось Х совпала с траекторией движения. Тогда движение точки может быть описано уравнением:

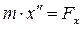, (1.86)

где F_x – сумма проекций всех сил на ось Х.

Масса m - величина постоянная, а сила F_x – величина переменная. Рассмотрим только те силы, которые могут зависеть от времени, скорости и координат положения точки приложения силы .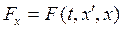

При решении и прямой, и обратной задач динамики используется уравнение (1.86). Решая прямую задачу, приходится выполнять операцию дифференцирования, а при решении обратной задачи – операцию интегрирования. Поскольку реальные законы движения и скорости материальных точек являются гладкими непрерывными функциями, то дифференцирование всегда осуществимо и, следовательно, прямая задача всегда может быть решена аналитически. А вот проинтегрировать можно далеко не всякую даже гладкую функцию, поэтому обратную задачу не всегда можно решить аналитически, ее решение сильно зависит от особенностей действующих сил.

Кроме того, операция интегрирования выполняется с точностью до константы, поэтому уравнение (1.86) необходимо дополнять начальными условиями. В любой задаче механики при решении обратной задачи начальные условия считаются заданными, если начальные значения отсутствуют, то можно принять любые значения.

1.3.4. Уравнения материальной точки в естественной системе координат

Если уравнение (1.84) разложить по осям естественной системы координат, получим:

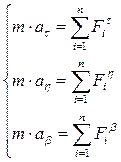, (1.87)

Учитывая особенности разложения вектора ускорений в естественной системе координат получим:

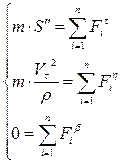, (1.88)

где S – закон движения в естественной системе координат.

1.3.5. Колебательное движение материальной точки

При движении материальной точки может действовать упругая сила, стремящаяся вернуть точку к некоторому положению. Эта упругая сила называется восстанавливающей. В большинстве задач рассматривается восстанавливающая сила F, изменяющаяся по линейному закону (закону Гука) (рис. 1.46). При растяжении пружины эта сила прямо пропорциональна удлинению:

F = -сΔ, (1.89)

где Δ — смещение конца пружины из ненапряженного состояния,

с — коэффициент упругости (коэффициент жесткости), численно равный силе, которую надо приложить к пружине для того, чтобы изменить ее длину на единицу, кг/см.

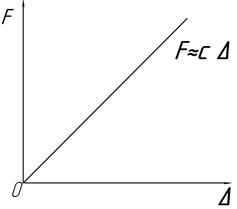
Рис. 1.46

Вообще линейной восстанавливающей называется сила, стремящаяся вернуть точку в положение равновесия и пропорциональная отклонению этой точки от положения равновесия.

Свободные колебания материальной точки.

Свободными называются колебания материальной точки, которые происходят под действием восстанавливающей силы. При движении материальной точки М массой m по горизонтальной оси х (рис. 1.47) под действием восстанавливающей силы F, равной по модулю 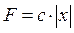(О-положение равновесия точки М), имеет место дифференциальное уравнение движения:

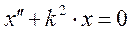, (1.90)

где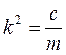

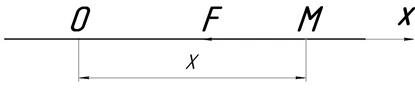
Рис. 1.47

При начальных условиях движения материальной точки, записанных в виде: t = 0, x = x₀, 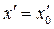закон ее свободных колебаний имеет вид:

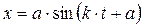(1.91)

т. е. материальная точка совершает гармоническое колебательное движение; а - амплитуда колебаний — наибольшее отклонение колеблющейся точки от положения равновесия:

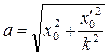(1.92)

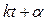- фаза колебаний; α – начальная фаза колебаний.

Периодом колебаний Т материальной точки называется наименьший промежуток времени, по истечении которого точка имеет ту же координату и ту же проекцию скорости:

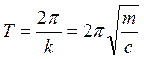. (1.93)

Вынужденные колебания материальной точки. Возмущающая сила.

В теории колебаний возмущающей называется сила, приложенная к материальной точке и заданная как функция времени. Эта сила большей частью является непрерывной функцией времени (рис. 1.48).

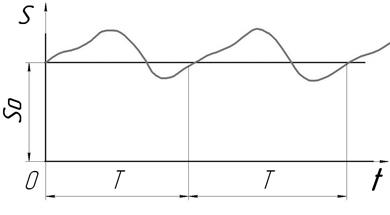
Рис. 1.48

В механизмах возмущающаяся сила возникает в результате неточной балансировки вращающихся частей машин (турбинных дисков, роторов электромоторов, маховиков), либо при наличии периодически изменяющейся силы давления воды, газа или пара в цилиндрах двигателей и т. д.

Простейшей является возмущающая сила S, изменяющаяся по гармоническому закону:

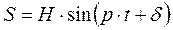(1.94)

где Н — наибольшая величина возмущающей силы (амплитуда силы), кг,

р — круговая частота изменения возмущающей силы, сек^-1,

δ — начальная фаза.

Вынужденные колебания материальной точки вызываются действием системы сил, в составе которой имеются восстанавливающая сила F и возмущающая сила S. На рис. 1.49 ось х направлена вдоль линий действия сил F и S. Начало отсчета выбрано в положении статического равновесия материальной точки. Сила S условно направлена вниз, однако, как следует из закона ее изменения, направление является переменным.

Дифференциальное уравнение вынужденных колебаний

материальной точки имеет вид:

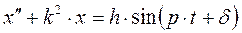, (1.95)

Рис. 1.49 где ,.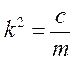

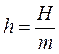
Амплитуда вынужденных колебаний а - величина наибольшего динамического смещения материальной точки, равна:

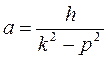(1.96)

1.3.6. Кинетическая энергия механической системы

Кинетическая энергия материальной точки – это половина произведения массы точки на её скорость:

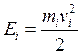, (1.97)

Кинетическая энергия механической системы– это сумма кинетических энергий всех точек системы:

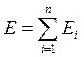. (1.98)

Теорема: кинетическая энергия тела, которое движется плоскопараллельно, равна сумме массы тела, умноженной на половину квадрата скорости центра масс тела и половине произведения собственного момента инерции тела на квадрат угловой скорости.

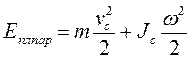. (1.99)

Следствия:

1. При поступательном движении тела его кинетическая энергия равна половине произведения массы тела на квадрат скорости любой точки тела.

Действительно, поступательное движение можно считать частным случаем плоскопараллельного при отсутствии вращения, т.е. при 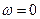. Кроме того, при поступательном движении скорости всех точек тела равны. Тогда из выражения (1.99):

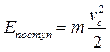, (1.100)

2. При вращательном движении тела его кинетическая энергия равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости.

Пусть тело вращается относительно оси, находящейся на расстоянии b от центра масс тела. Тогда скорость центра масс:

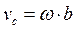, (1.101)

Из формулы (1.99) будем иметь:

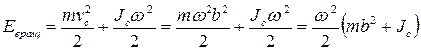. (1.102)

Выражение в скобках есть момент инерции относительно действительной оси вращения.

1.3.7. Работа

Элементарная работа силы – это скалярное произведение силы на вектор элементарного перемещения точки приложения силы:

, (1.103)

где 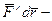угол между направлением действия силы и направлением элементарного перемещения.

Из формулы видно, что:

- если направления силы и перемещения совпадают, то работа равна произведению силы на перемещение;

- если направления силы и перемещения перпендикулярны друг другу, то работа равна нулю;

- если угол между силой и перемещением больше прямого угла, то работа силы будет величиной отрицательной.

Полная работа силы на конечном перемещении – это сумма всех элементарных работ данной силы

. (1.104)

Приведем несколько случаев определения работ для разного вида сил. Для простоты будем считать, что сила и перемещение совпадают по направлению. Если это не так, то результат надо умножить на косинус соответствующего угла.