Скорость
В некоторый момент времени t0 положение точки характеризует радиус-вектор 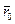 , а через некоторое время
, а через некоторое время 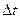 в момент t1=t0+
в момент t1=t0+ 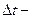
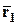 (рис. 1.29). Если через концы векторов
(рис. 1.29). Если через концы векторов 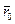 и
и 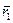 провести новый вектор
провести новый вектор 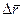 , то получим равенство
, то получим равенство
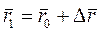 . (1.29)
. (1.29)
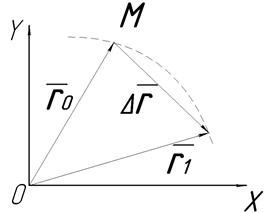
Рис. 1.29
Средняя скорость движения - это изменение положения материальной точки за промежуток времени, в течение которого это изменение произошло:
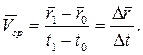 (1.30)
(1.30)
Мгновенная скорость (в дальнейшем просто скорость) - это предел средней скорости при бесконечном уменьшении промежутка времени наблюдения, т. е.:
 .(1.31)
.(1.31)
Таким образом, скорость – это первая производная от закона движения по времени (третья характеристика движения). Скорость является векторной величиной, и ее направление совпадает с направлением вектора в его предельном положении, т. е. вектор скорости всегда располагается на касательной к траектории движения и направлен в ту сторону, куда происходит движение. Чтобы определить, величину скорости (модуль), необходимо разложить вектора 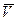 и
и  на составляющие в выбранной системе координат, т.е. представить
на составляющие в выбранной системе координат, т.е. представить 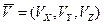 и
и 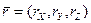 .Тогда между компонентами скорости и радиус-вектора положение точки должно выполняться соотношение:
.Тогда между компонентами скорости и радиус-вектора положение точки должно выполняться соотношение:
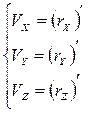 (1.32)
(1.32)
В этом случае модуль скорости можно определить как:
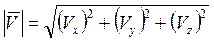 (1.33)
(1.33)
Дата добавления: 2015-02-10; просмотров: 897;
