Координаты центра тяжести.

Силу тяжести фактически можно считать системой параллельных сил, поэтому для нее применимы все выше приведенные формулы.

Если тело является однородным, т.е. плотность его в любой точке тела одинакова, получаем, что вес элементарного объема тела определяется по формуле:

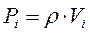, (1.20)

где 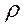- плотность тела,

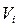- объем i-ой части тела.

Тогда координата точки С по оси Х (остальные координаты находятся аналогично):

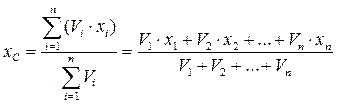, (1.21)

Если тело является плоским и однородным, то:

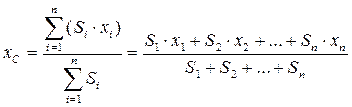, (1.22)

где 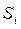- площадь i-ой части тела.

1.1.11. Трение

Трение скольжения

В местах контакта реальных тел возникает сила, сопротивляющаяся взаимному смещению контактирующих поверхностей – сила трения. Она всегда направлена по касательной к контактирующим поверхностям и всегда стремится препятствовать суммарной внешней силе.

Важнейшее свойство сил трения - это то, что они не могут вызывать движения. При отсутствии внешних сил, сила трения всегда равна нулю. При достаточно малой суммарной внешней силе, сила трения будет в точности равна ей по модулю и противоположна по направлению. При возрастании внешних сил, сила трения может их компенсировать только до определенного момента, а затем состояние равновесия тела нарушается и оно приходит в движение.

Состояние тела, когда малейшее увеличение внешней силы вызовет нарушение равновесия тела называют предельным равновесием, а сила трения, действующая на тело в этот момент времени предельной силой трения.

Величина предельной силы зависит от многих факторов: от материала контактирующих тел, от чистоты обработки контактирующих поверхностей, от температуры окружающей среды и т.д., но примерно можно определить предельную силу трения, как:

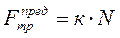, (1.23)

где 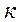- статический коэффициент трения, зависящий только от материала и состояния контактирующих тел, определяемый экспериментально;

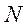- величина нормального давлении между контактирующими поверхностями.

Конус трения.

Рассмотрим предельное равновесие тела (пренебрегая его собственным весом), покоящегося на шероховатой поверхности и к которому приложена некоторая сила Р (рис. 1.20).

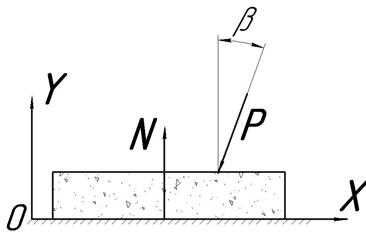
Рис. 1.20

Составим уравнения равновесия

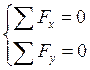
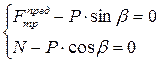, (1.24)

Учитывая определение предельной силы трения, найдем величину силы 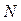из уравнения (1.23) и подставим в уравнение (1.24):

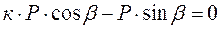, (1.25)

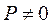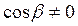а поскольку и , то в случае предельного равновесия должно выполняться равенство

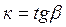или 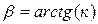. (1.26)

Угол, определяемый соотношением (1.26), называют предельным углом трения. Если к телу прикладывать какую угодно большую силу, но под углом меньшим предельного угла b, то нарушить состояние покоя тела невозможно.

Если рассмотреть пространственную задачу, то получим предельный конус трения, показывающий, что, если сила действует внутри этого конуса, тело сохранит состояние покоя. В технике такое явление называется заклиниванием механизма.

Трение качения

Рассмотрим цилиндрическое тело, покоящееся на шероховатой поверхности к которому приложена некая внешняя сила Р (рис. 1.21. а).

Силы Р и F_тр образуют пару сил с моментом 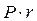, который ничем не компенсирован и, следовательно, при любой малой силе Р должно начинаться движение тела. Но на практике это не так. Тело начнет движение только при определенном значении силы Р.

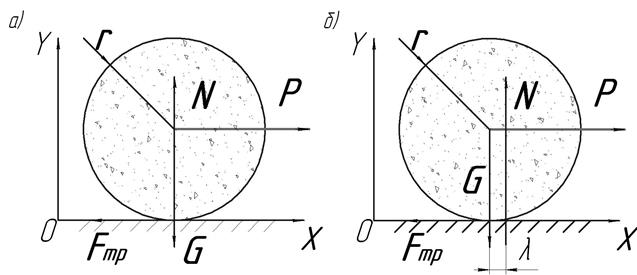
Рис. 1.21

Это объясняется тем, что у реальных тел контакт осуществляется не в точке, а всегда по определенной поверхности и поэтому реакцию N необходимо прикладывать не к середине поверхности контакта, а на ее краю (рис. 1.21. б). В этом случае силы N и G образуют пару сил, противодействующую паре сил Р и F_тр.

Момент пары сил N и G называют моментом трения качения, а в случае предельного равновесия это будет предельный момент трения качения:

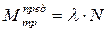, (1.27)

где l - коэффициент трения качения, зависящий только от материала контактирующих тел, определяемый экспериментально.

Физический смысл коэффициента трения качения заключается в том, что он представляет собой полуширину поверхности контакта (рис. 1.21. б).

Также как и силы трения скольжения, силы трения качения всегда противодействуют суммарному моменту внешних сил.

Поскольку для материалов 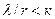, то потери энергии при трении качения меньше, чем при скольжении поэтому желательно заменять скольжение качением.

При решении задач на трение после определения реакций связи, включающих F_тр и М_тр, необходимо дополнительно проверять выполнение услови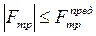й:

и 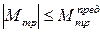, (1.28)

Если эти условия не выполняются, то равновесие невозможно.

1.1.12. Пример решения задачи на использование условий равновесия

плоской системы сходящихся сил.

Определить реакции стержней, удерживающих грузы F₁ и F₂ (рис. 1.22). Массой стержней пренебречь. Выполним проверку полученных результатов графическим и аналитическим способами. Числовые данные варианта взять из приложения 1. Схему варианта из приложения 2.

Схема нагружения и исходные данные

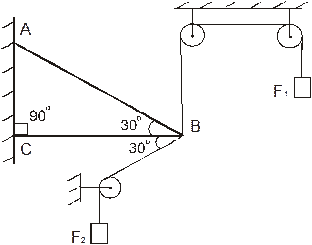
F₁ = 0,5 кН,

F₂ = 0,8 кН

Рис. 1.22.

Решение

Составим расчетную схему, для чего избавимся от связей. Проведем оси координат, причем ось х проходит через неизвестную внутреннюю силу (рис. 1.23).

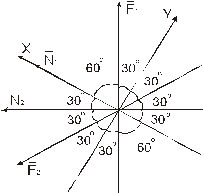
Рис. 1.23. Составим систему уравнений равновесия плоской

системы сходящихся сил и решим ее.

∑F_ix=0 N₁ + N₂cos 30⁰ + F₁cos60⁰ + F₂cos60⁰=0

∑F_iy=0 - N₂cos 60⁰ + F₁cos30⁰ - F₂cos30⁰=0

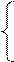N₁ = - N₂cos 30⁰ - F₁cos60⁰ - F₂cos60⁰

N₂ = (F₁cos30⁰ - F₂cos30⁰)/cos 60⁰

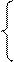N₁ = -N₂∙0,866 - 0,5∙0,5 - 0,8 ∙ 0,5 N₁= - 0,2 кН

N₂ = (0,5∙0,866 - 0,8 ∙ 0,866)/0,5 N₂= -0,5 кН

Знак «–» указывает на то, что стержни АВ и СВ сжаты.

Проверка аналитическим способом.

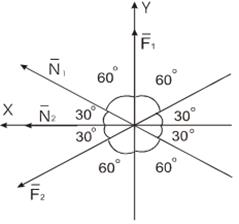
Рис. 1.24.

Выберем новую систему координат (рис. 1.24) и составим новую систему уравнений равновесия.

∑F_ix=0 N₁cos 30⁰ + N₂ + F₂cos30⁰ = 0 N₂ = - N₁cos 30⁰ - F₂cos30⁰

∑F_iy=0 F₁ - F₂cos 60⁰+ N₁cos 60⁰ = 0 N₁ = (F₂cos60⁰ - F₁)/cos60⁰

N₂ = -N₁∙0,866 - 0,8∙0,866 N₂ = - 0,5 кН

N₁ = (0,8∙0,5-0,5)/0,5 N₁ =- 0,2 кН

Ответы совпадают, следовательно, задача решена верно.

Проверка графическим способом. Построим силовой многоугольник (рис. 1.25), для чего из точки В, в масштабе отложим отрезок ВА соответствующий величине силы F₂. Из конца отрезка ВА отложим под углом 60⁰ отрезок АС соответствующий величине силы F₁, вследствие того что угол между линиями действия сил F₁ и F₂ составляет 60⁰. Так как величины сил N₁ и N₂ неизвестны, то построим прямые а и в, причем отложим прямую а под углом 90⁰ к отрезку АС, прямую в по углом 120⁰ к отрезку ВА. Прямые а и в пересекутся в точке D. Длина отрезка CD соответствует силе N₂, а длина отрезка DВ силе N₁. Переведя в масштабе длины отрезков CD и DВ получим числовые значения искомых сил. N₁=0,2 кН; N₂=0,5 кН.

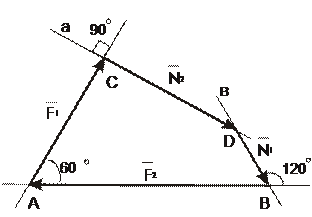
Рис. 1.25.

1.1.13. Пример определения реакций опор двухопорной балки.

На использование условий равновесия плоской произвольной системы сил.

Определить реакции опор двух опорной балки (рис. 1.26). Выполнить проверку. Числовые данные варианта взять из приложения 3. Схему варианта из приложения 4.

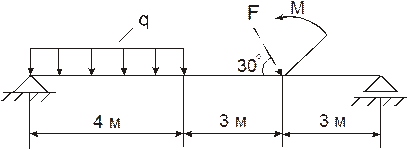Схема нагружения и исходные данные.

q = 4,5 н/м.

F = 65 Н.

М = 45 Н∙м.

Рис. 1.26.

Решение.

Составим расчетную схему.

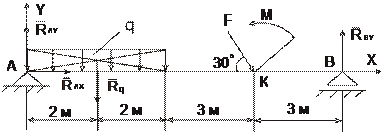
Рис 1.27.

Преобразуем распределенную нагрузку q в сосредоточенную силу R_q и определим ее величину: R_q = 4 ∙ 4,5 = 18 [Н].

Составим систему уравнений равновесия произвольной плоской системы сил и решим ее.

∑F_ix = 0 R_АХ + Fcos30⁰ = 0

∑F_iy = 0 R_АY - Fcos60⁰ - R_q + R_BY = 0

∑М_А = 0 R_BY∙10 + M - Fcos60⁰ ∙ 7- R_q ∙ 2 = 0

R_АХ = - 65 ∙ 0,866 R_АХ = -56,29 Н

R_АY = 65 ∙ 0,5 + 18 - R_BY R_АY = 28,65 Н

R_BY = (- 45 + 65 ∙ 0,5 ∙7 + 18 ∙ 2)/10 R_BY = 21,85 Н

Отрицательное значение реакции R_АХ указывает на то, что ее направление было выбрано не верно, то есть необходимо на расчетной схеме направить ее в противоположную сторону.

Проверка.

Составим уравнение моментов относительно точки К.

∑М_К = 0

R_BY∙3 + М + R_q∙5 - R_АY∙7 = 0

21,85 ∙ 3 + 45 + 18 ∙ 5 - 28,65 ∙ 7 = 0

0 = 0

Результат свидетельствует о том, что задача решена верно.