Сложное сопротивление

2.6.1. Косой изгиб

Если в поперечном сечении возникают два внутренних силовых фактора – изгибающие моменты М_x и M_y , то происходит косой чистый изгиб. При поперечном косом изгибе в поперечных сечениях бруса одновременно с изгибающими моментами возникают поперечные силы Q_x и Q_y . В том и другом случае нормальное напряжение σ в любой точке К поперечного сечения (рис. 2.39), согласно принципу независимости действия сил, определяется как алгебраическая сумма напряжений, обусловленных изгибающими моментами М_x и M_y т.е.:

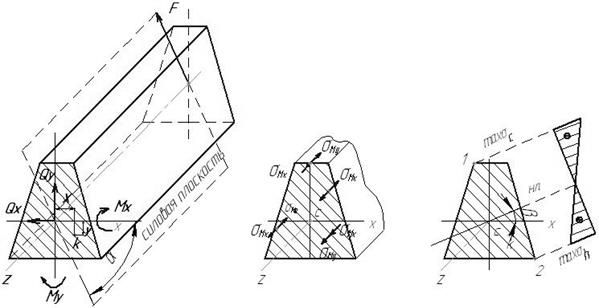
Рис. 2.39.Косой изгиб

. (2.38)

В зависимости от нагружения бруса слагаемые напряжения направлены, в разных четвертях, поперечного сечения либо в одну и ту же, либо в противоположные стороны. Чтобы определить точки сечения, в которых напряжения достигают наибольших значений, необходимо найти положение нулевой линии. Для этого приравняем последнее выражение нулю и заменим у и х координатами у₀ и х₀, принадлежащими нулевой линии. В результате получаем уравнение нулевой линии:

(2.39)

Это уравнение показывает, что нулевая линия – прямая, проходящая через начало координат под углом β к оси х, тангенс которого:

. (2.40)

Определив угол β и прочертив нулевую линию в поперечном сечении можно определить координаты наиболее удаленных точек 1 и 2 и вычислить значения напряжений в этих точках.

Для бруса из материала, различно сопротивляющегося растяжению и сжатию должны быть составлены два условия прочности:

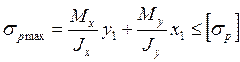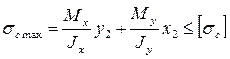. (2.41)

Для брусьев из пластичных материалов используют лишь то из условий, которое соответствует большему по абсолютному значению напряжения.

2.6.2. Главные площадки и главные напряжения

Рис. 2.40. Сложное сопротивление

Рассмотрим вырезанный из тела элемент в виде прямоугольного параллелепипеда. На гранях возникают нормальные и касательные напряжения. Оказывается, что через заданную точку напряженного тела всегда можно провести три взаимно перпендикулярные плоскости, в которых касательные напряжения: 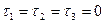и возникают только нормальные напряжения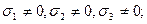 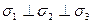(рис. 2.40);

Площадки, на которых нет касательных напряжений – это главные площадки, а нормальные напряжения – это главные напряжения.

Если 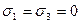, то:

Такой случай называется простым, одноосным напряженным состоянием (растяжение или сжатие).

2.6.3. Тензор напряжений

Разложим каждый вектор напряжений на составляющие вдоль координатных осей (рис. 2.41). На каждой площадке действует одно нормальное напряжение σ_x; σ_y; σ_z где индекс обозначает направление вектора нормали к площадке и два касательных напряжения τ с двумя индексами, из которых первый указывает направление действия компоненты напряжения, второй направление вектора нормали к площадке.

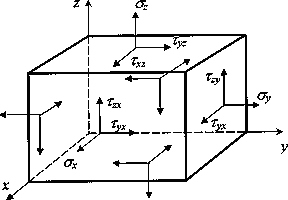
Рис. 2.41. Составляющие векторов напряжений

Совокупность девяти компонент напряжений (по три на каждой из трех взаимно перпендикулярных площадок) представляет собой некоторый физический объект, называемый тензором напряжений в точке. Тензор можно представить в виде матрицы, соответствующим образом упорядочив девять компонент:

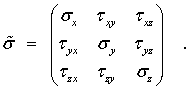
Для компонент тензора напряжений общепринятым является следующее правило знаков: компонента считается положительной, если на площадке с положительной внешней нормалью (т. е. направленной вдоль одной из координатных осей), эта компонента направлена в сторону положительного направления соответствующей оси. На рис. 2.41 все компоненты тензора напряжений изображены положительными. На площадках с отрицательной внешней нормалью (грани параллелепипеда, невидимые на рис. 2.41) положительная компонента направлена в противоположном направлении. Напряжения на трех взаимно ортогональных площадках с отрицательными направлениями нормалей также характеризуют напряженное состояние в точке. Эти напряжения, являющиеся компонентами тензора напряжений, определяются аналогично напряжениям на площадках с положительной нормалью. Они обозначаются теми же символами и имеют положительное направление, обратное изображенному на рис. 2.41.

2.6.4. Изгиб с растяжением-сжатием

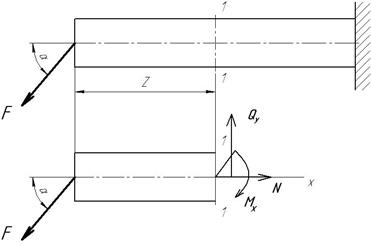
Рис. 2.42. Схема изгиба с растяжением – сжатием

Если нагрузить брус в главной плоскости силой F под углом α к оси, то в поперечном сечении 1-1 возникнут три внутренних силовых фактора: нормальная сила 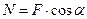, изгибающий момент 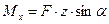и поперечная сила 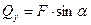. Такое нагружение бруса вызывает сочетание изгиба с растяжением – сжатием (рис. 2.42). Влияние поперечных сил на прочность бруса обычно не учитывают.

Считая, что брусья обладают большой жесткостью на изгиб, согласно принципу независимости действия сил, можно утверждать, что в любом сечении возникают напряжения растяжения (или сжатия):

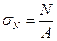и напряжения изгиба:

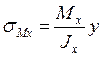(2.42)

Таким образом, суммарные напряжения в любом сечении бруса находят алгебраическим сложением напряжений при растяжении и изгибе:

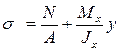(2.43)

При расчетах на прочность исходят из наибольших напряжений, возникающих в любом сечении. В частности, если сечение бруса симметрично относительно нейтральной оси, то:

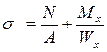(2.44)

При определении напряжений по приведенным формулам значения напряжений следует подставлять с их знаками.

2.6.5. Теории прочности

В отличие от простых видов деформации, на практике, часто встречается, когда в поперечном сечение бруса возникает несколько внутренних силовых факторов (изгиб и кручение) – что называется сложным сопротивлением.

Расчеты на прочность и жесткость основываются на принципе независимости действия сил. Оценка прочностной надежности является распространенной инженерной задачей, в которой напряженное состояние в опасной точки элемента конструкции сопоставляется с предельным состоянием, определенным пределом тягучести, прочности и т.д., для материала этого элемента конструкции. Такая оценка точная, когда в одноосном или двухосном состоянии, главные напряжения в каждой точке равны по величине, но разные по знаку.

Первая теория прочности

Теория наибольших нормальных напряжений

Она основывается на предположениях, что опасное состояние материала наступает, когда какое – либо из главных напряжений достигает опасного значения, следовательно, сложно – напряженное состояние равноопасно если 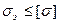, т.е. максимальное напряжение не превышает допускаемое.

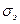-эквивалентное допускаемое напряжение; 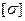-допускаемое напряжение при растяжении.

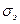
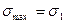= (2.45)

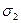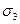Недостатки: она не учитывает напряженность и , подтверждает деформацию хрупких и не подтверждает деформацию пластичных материалов.

Вторая теория прочности

Теория наибольших линейных деформаций

Основывается на предположении, что материал не зависимо от вида напряженного состояния разрушается, тогда когда наибольшее относительное удлинение или укорочение, в каком-либо направлении достигает такой величины, при которой идет разрушение как при простом растяжении – сжатии.

Условие прочности:

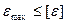, (2.46)

где 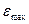-наибольшая относительная деформация; 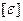- допускаемая относительная деформация.

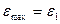, (2.47)

где 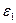- деформация, в направлении 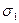, переходя от деформации к напряжению (закон Гука) получим:

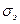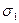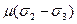= = , (2.48)

.

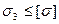Из уравнения видно, что с допускаемым напряжением необходимо сравнивать комбинацию напряжений.

Вторая теория учитывает влияния всех трех главных напряжений и опытами подтверждается деформация хрупких материалов.

Третья теория прочности

Теория касательных напряжений

В качестве фактора определяющего прочность материала принимается величина наибольшего касательного напряжения. Предполагается, что предельное напряженное состояние наступит тогда, когда наибольшее касательное напряжение достигнет опасного значения, соответствующего предельному состоянию данного материала при растяжении.

,

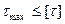где 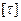- допускаемое напряжение при растяжении.

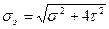. (2.49)

В третьей теории прочности подтверждается экспериментально деформация пластичных материалов.

Недостаток теории: она не учитывает главные напряжения 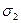, которые оказывают влияние на прочность материала. Третья теория прочности не применима для расчета деталей из хрупких материалов.

Четвертая теория прочности

Предельное (опасное) состояние наступает в тот момент, когда на некоторой площадке возникает наиболее неблагоприятная комбинация касательных и нормальных напряжений.

Условие прочности имеет вид:

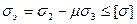, (2.50)

где 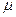- коэффициент, равный отношению предельных напряжений при осевом растяжении и сжатии.

Для пластичных материалов 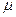=1.

Теория прочности Мора совпадает с третьей теорией.

Ее недостаток состоит в том, что она не учитывает влияния на прочность напряжения .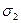

Пятая теория прочности Мора

Энергетическая теория формоизменения

В качестве критерия прочности в данном случае принимается количество удельной потенциальной энергии формоизменения, накопленных деформацией элементов. Переход материала в предельное состояние происходит, когда величина удельной потенциальной энергии формоизменения достигнет значения соответствующее предельному состоянию данного материала.

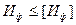(2.51)

где 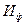-удельная потенциальная энергия формоизменения;

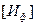-допускаемая потенциальная энергия формоизменения.

- для общего вида

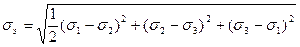, (2.52)

Для случая кручения и изгиба:

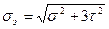. (2.53)

2.6.6. Изгиб с кручением

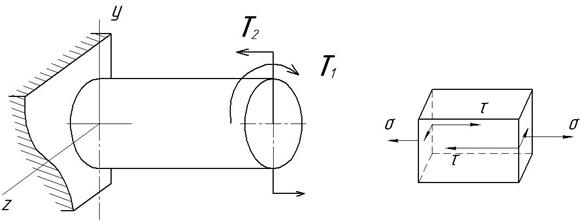
Рис. 2.43.Изгиб с кручением

Возьмем стальной брус круглого поперечного сечения, который нагружен двумя парами сил, таким образом, что плоскость действия первой перпендикулярна оси бруса, а плоскость действия второй проходит через ось бруса (рис. 2.43). Тогда момент Т₁ первой пары скручивает брус, а момент Т₂ второй пары его изгибает. При таком нагружении бруса в его поперечных сечениях возникают два внутренних силовых фактора – крутящий М_к и изгибающий М_и моменты, причем по всей длине бруса М_к= Т₁, а М_и= Т₂.

Выразим эквивалентные напряжения через касательные и нормальные напряжения в поперечном сечении бруса по третьей и пятой теории:

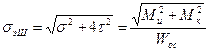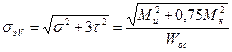; . (2.54)

Арифметическое значение корней в числителях этих формул иногда называют эквивалентным моментом, и обозначают М_э. Используя это обозначение, условие прочности запишем в таком виде:

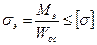. (2.55)

При этом надо иметь в виду, что при пространственном нагружении вала, например в вертикальной и горизонтальной плоскостях, будут возникать два изгибающих момента – М_х и М_у , тогда изгибающий момент М_ибудет равен:

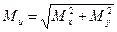. (2.56)

2.6.7. Пример расчета вала на изгиб с кручением

Вал передает мощность Р при угловой скорости вращения ω. Определите диаметр опасного сечения вала, несущего шкив ременной передачи диаметром d₁ и зубчатое колесо с косыми зубьями диаметром d₂. Натяжение ведущей ветви ремня вдвое больше натяжения ведомой F₁ = 2F₂. В зацеплении на зубчатое колесо действуют силы: окружная F_t, направленная по касательной к делительной окружности колеса, осевая F_a, направленная параллельно оси вала, и радиальная F_r – направленная по радиусу к центру зубчатого колеса. Материал вала – сталь 45, [σ] = 65 МПа. Расчет выполнить, используя гипотезу наибольших касательных напряжений. Принимаем F_r = 0,38F_t, F_a = 0,2F_t.

Числовые данные варианта взять из приложения 15, схему варианта из приложения 16.

Исходные данные.

Диаметр, мм Мощность, кВт Угловая скорость, рад/с Длина, м Угол, град

d₁ d₂ Р w а α

0,1

Решение:

1. Составляем расчетную схему вала (рис. 2.44.).

Точка С. Перенесем силы F₁ и F₂, действующие на шкив 1 параллельно самим себе к продольной оси вала, присоединив при этом пары сил с моментами F₁·d₁/2 и F₂·d₂/2. Имеем центральную силу F= F₁+F₂·= 3F₂, изгибающую вал в плоскости под углом α к горизонтальной плоскости и скручивающий момент

М_е₁ = F₁·d₁/2 – F₂·d₂/2 = 2·F₂·d₁/2 – F₂·d₁/2 = F₂·d₁/2

Точка D. Проведем к оси вала силы, действующие на зубчатое колесо 2:

перенесем силу F_t параллельно самой себе на ось вала, присоединив при этом момент пары сил равный F_t·d₂/2. Моментом пары является вращающий момент М₂, а центральная сила F_t изгибает вал в горизонтальной плоскости. Кроме силы F_t действуют сила F_r, изгибающая вал в вертикальной плоскости и сила F_a, перенесенная на ось вала с присоединенной противонаправленной силой F_a создает изгибающий момент в вертикальной плоскости равный F_a·d₂/2.

Для дальнейших расчетов представим вал как балку на двух опорах, рассматривая подшипники А и В как шарнирные опоры, одна из которых имеет продольную неподвижность.

2. Определяем момент, передаваемый валом, по заданной мощности Р и угловой скорости ω:

М = Р/ω = 80·10³/70 = 1142,9 Н·м

Крутящий момент в сечениях вала на участке CD определяем методом сечений: М_к = М

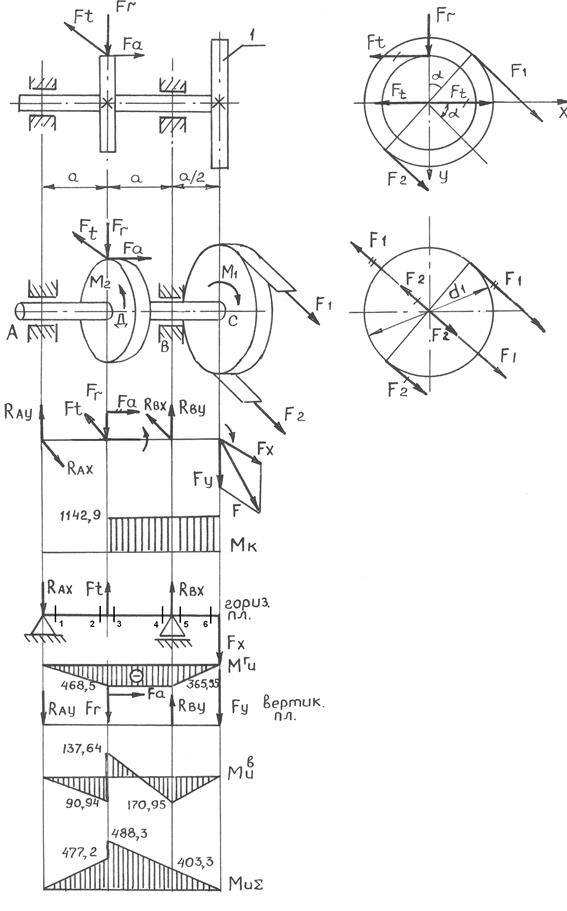
Рис. 2.44. Расчет наизгиб с кручением

3. Определяем силы натяжения ремней и силы, возникающие в зацеплении зубчатой передачи. Из равенства вращающих моментов М= М₁= М₂ находим силу натяжения ветвей ременной передачи:

F₂ = 2·М/d₁ = 2·1142,9/0,85 = 2689 Н

F₁= 2·F₂=5378 Н

Силы в зацеплении зубчатого колеса:

Окружная сила F_t = 2M/d₂ = 2·1142,9/0,4 = 5714,5 Н

Радиальная сила F_r = 0,38·F_t = 0,38·5714,5 = 2171,5 Н

Осевая сила F_a = 0,2·F_t = 0,2·5714,5 = 1142,9 Н.

4. Определяем силы изгибающие вал в горизонтальной и вертикальной плоскостях и строим эпюры изгибающих моментов. Силы в зацеплении зубчатой передачи действуют строго в горизонтальной (F_t) и вертикальной (F_a, F_r) плоскостях.

На шкиве силы натяжения ремня действуют под углом α, поэтому их равнодействующую раскладываем на горизонтальную и вертикальную составляющие:

F = F₁ + F₂ = 5378 + 2689 = 8067 Н

F_x = F·cos 25° = 7311 Н

F_y = F·sin 25° = 3409 Н

Рассмотрим изгиб вала в горизонтальной плоскости. Находим реакции опор R_AX и R_BX

Σ М_А = 0 -F_x·2,5a + R_BX ·2а + F_t·a = 0

R_BX = (2,5·F_x – F_t)/2 = (2,5·7311 – 5714,5)/2 = 6281,5 H

ΣМ_В = 0 R_AX·2a – F_t·a – F_x·0,5a = 0

R_AX = (F_t + 0,5·F_x)/2 = (5714,5 + 0,5·7311)/2 = 4685 H.

Проверка Σ F_ix = 0

- R_AX + F_t + R_BX- F_x = 0

- 4685 + 5714,5 + 6281,5 – 7311 = 0 0 = 0

Строим эпюру изгибающих моментов

1:1 M₁=0 ;

2:2 M₂= - R_AX·а = - 4685·0,1 = - 468,5 Нм

3:3 M₃=M₂ = -468,5 Hм

4:4 M₄= - R_AX·2а+ F_ta = - 4685·0,1+5714,5·0,1= - 365,5 Hм

(рассматриваем правую сторону)

5:5 M₅=-F_x·a·0,5 = - 7311·0,1·0,5 = - 365,5 Hм

6:6 M₆=0

Вычислим реакции опор R_AY и R_BY

Σ М_А = 0 - F_r·a – F_a·0,5d₂ + R_B_у·2а – F_y·2,5a = 0

R_BY = (2171,5·0,1+1142,9·0,5·0,4+3409·2,5·0,1)/2·0,1 = 6489,9 Н

Σ М_В = 0 R_Ау·2а + F_r·a – F_a·0,5d₂ – F_y·0,5a = 0

R_AY = (-2171,5·0,1+1142,9·0,5·0,4+3409·0,5·0,1)/2·0,1 = 909,4 Н

Σ F_iу = 0 - R_Ау – F_r- F_y + R_Bу= 0

-909,4 - 2171,5 – 3409 – 6489,9 = 0; 0 = 0

Строим эпюру изгибающих моментов в вертикальной плоскости:

1:1 M₁=0

2:2 M₂=- R_AY·а = - 909,4·0,1 = - 90,9 Нм

3:3 M₃=- R_AY·а+F_a·d₂/2= - 90,9+1142,9·0,4/2 = 137,6 Hм

4:4 M₄= - R_Ay·2а- F_ra+ F_a·d₂/2= - 909,4·0,1·2+2171,5·0,1+1142,9·0,4/2 = -170,9 Hм

(рассматриваем правую сторону)

5:5 M₅= - F_y·a·0,5=-3409·0,1·0,5 = - 170,9 Hм

6:6 M₆=0

Строим суммарную эпюру изгибающих моментов:

М_И =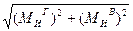

1:1 М₁ = 0

2:2 М₂ = 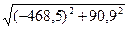= 477,2 Нм

3:3 М₃ = 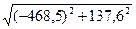= 488,3 Нм

4:4 М₄ = 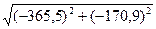= 403,3 Нм 5:5 М₅ = M₄ = 403,3 Hм 6:6 М₆ = 0

Определим положение опасного сечения, анализируя эпюры суммарного изгибающего М_И и крутящего М_К моментов. Это сечение 3:3 в точке D.

5. Определяем диаметр вала. Расчет производим для опасного сечения. Эквивалентный момент в опасном сечении посчитываем с использованием гипотезы наибольших касательных напряжений:

М_экв^D= 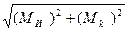= = 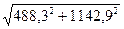1242,8 Нм

Диаметр вала из условия прочности при изгибе с кручением:

σ_max = М_э/W_x ≤ [σ], W_x = π·d³/32 = 0,1·d³

d = 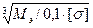= = 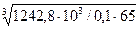57,6 мм.

Учитывая ослабление вала шпоночными канавками, округляем диаметр до большей стандартной величины.

Принимаем d = 60мм.

2.7. Устойчивость сжатых стержней

Стержень при сжимающей осевой силе, меньше критического значения находится в состояние устойчивого равновесия (рис. 2.45. а).

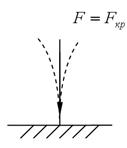
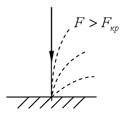
а. б. в.

Рис. 2.45.Устойчивость сжатых стержней.

При значении сжимающей силы, превосходящем определенную величину прямолинейная форма равновесия становится неустойчивой и сменяется криволинейной формой равновесия, которая оказывается при этом устойчивой (рис. 2.45. б).

Наименьшее значение сжимающей силы, при которой сжатый стержень теряет способность сохранять прямолинейную форму равновесия, называется критической силой (рис. 2.46. в). По определению Эйлера, критической называют силу 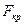требующуюся для самого малого наклонения колонны.

Исследования показывают, что пока сжимающая сила меньше критической, прогибы стержня будут небольшими. Но при приближении значения силы к критическому они начинают неограниченно возрастать. Этот критерий (неограниченный рост изгибов, при ограниченном росте сжимающей силы), принят за критерий потери устойчивости. В целях безопасности допускаемая нагрузка должна быть меньше критической:

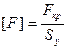, (2.57)

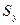- коэффициент запаса устойчивости.

Формула Эйлера:

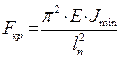. (2.58)

где Е – модуль упругости; 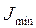-наименьший из осевых моментов инерции сечения;

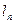-приведенная длина стержня, 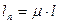, -коэффициент приведения длины стержня, коэффициент Ясинского.

Коэффициент Ясинского зависит от способа закрепления концов стержня (рис. 2.46.).

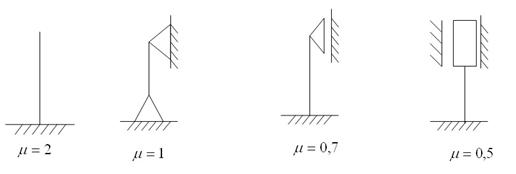
Рис. 2.46. Способы закрепления концов стержня.

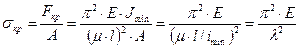, (2.59)

где 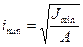- минимальный радиус инерции сечения, 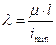- гибкость стержня

Формула Эйлера справедлива только в пределах применимости закона Гука, т.е. до тех пор, пока критическое напряжение не превышает предела пропорциональности материала стержня, т.е. при условии:

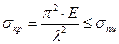отсюда 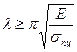. (2.60)

Стоящая в правой части неравенства постоянная для данного материала безразмерная величина называется предельной гибкостью:

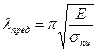. (2.61)

Таким образом, применимость формулы Эйлера определяется условием:

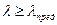. (2.62)

Формула Эйлера применима только в тех случаях, когда гибкость стержня больше или равна предельной гибкости того материала, из которого он изготовлен.

Формула Ясинского, применяется в случаях, когда не применима формула Эйлера.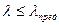

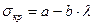, (2.63)

где a, b – коэффициенты, зависящие от материала (определяются экспериментально)

2.8. Усталостное разрушение

При действии на детали машин повторных переменных нагрузок происходит их разрушение в результате постепенно развивающихся трещин, они называются трещинами усталости.

Природа усталостного разрушения обусловлена особенностями молекулярного и кристаллического строения вещества. При повторных – переменных нагрузках появляется наклеп, и повышается хрупкость материала. Затем способность материала к упрочнению исчерпывается и возникает микротрещина. Возникающая трещина сама становится концентратором напряжения и с учетом увеличивающегося ослабления сечения становится местом окончательного разрушения.

Усталость – накопление необратимых изменений в материале при приложении циклических нагрузок.

Разрушение в результате постепенного развития трещины – усталостное разрушение.

Выносливость материала– способность материала сопротивляться разрушению при действии циклических нагрузок.

Цикл– однократная смена напряжения.

Рис. 2.47. Предел выносливости

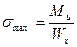
Наибольшее значение максимального по величине напряжения цикла, которому материал может сопротивляться без разрушения неограниченно долго, называется пределом выносливости (рис. 2.47.).

Контроль знаний студентов осуществляется на рубежных контролях в виде компьютерного тестирования, список тестовых вопросов приведен в приложении 9.

ЧАСТЬ ТРЕТЬЯ

<14 15 161718 19 20 >

Дата добавления: 2015-02-10; просмотров: 1725;

Диаметр, мм	Мощность, кВт	Угловая скорость, рад/с	Длина, м	Угол, град
d₁	d₂	Р	w	а	α
				0,1