Лекция №20. Треугольники сопротивлений, напряжений и мощностей. Треугольники сопротивлений, напряжений и мощностей.
Цель: расширить и углубить знания студентов по цепям синусоидального тока.
Задача: научить применять полученные знания для расчета цепей.
Выражение для нахождения полного сопротивления Z. По формуле
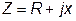 .
.
Из этого следует, что модуль комплексного сопротивления:

 . (3.44)
. (3.44)
Следовательно, z можно представить как гипотенузу прямоугольного треугольника (рис. 3.13) – треугольника сопротивлений, один катет которого равен R, другой - х.
При этом
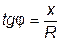 , (3.45)
, (3.45)
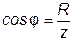 . (3.46)
. (3.46)
Зная 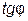 или
или 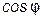 , можно определить угол
, можно определить угол 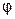 .
.
 Знак угла
Знак угла 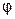 в выражениях для мгновенного значения тока
в выражениях для мгновенного значения тока 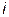 определяется характером нагрузки: при индуктивном характере нагрузки (
определяется характером нагрузки: при индуктивном характере нагрузки ( 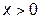 ) ток отстаёт от напряжения на угол
) ток отстаёт от напряжения на угол 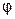 и в выражении для мгновенного значения тока угол
и в выражении для мгновенного значения тока угол 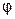 записывают со знаком минус, то есть
записывают со знаком минус, то есть 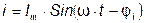 ; при емкостном характере нагрузки (
; при емкостном характере нагрузки ( 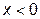 ) ток опережает напряжение на угол
) ток опережает напряжение на угол 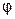 и выражение мгновенного значения тока записывают со знаком плюс, то есть
и выражение мгновенного значения тока записывают со знаком плюс, то есть 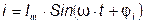 .
.
 Ранее были рассмотрены характеры напряжений на резисторе, конденсаторе и катушке. И было отмечено, что на сопротивлении ток и напряжение по направлению совпадают, на индуктивности напряжение опережает ток на 900, а на ёмкости напряжение отстаёт от тока на 900, то есть должно быть повернуто относительно вектора тока на угол 900 в отрицательном направлении (а на индуктивности в положительном). Это отображено на рис. 3.14.
Ранее были рассмотрены характеры напряжений на резисторе, конденсаторе и катушке. И было отмечено, что на сопротивлении ток и напряжение по направлению совпадают, на индуктивности напряжение опережает ток на 900, а на ёмкости напряжение отстаёт от тока на 900, то есть должно быть повернуто относительно вектора тока на угол 900 в отрицательном направлении (а на индуктивности в положительном). Это отображено на рис. 3.14.
Из этого видно, что при последовательном соединении R, L, C суммарное напряжение будет равно векторной сумме 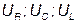 возможны три случая различных значений реактивного сопротивления и, соответственно, три значения суммарного напряжения.
возможны три случая различных значений реактивного сопротивления и, соответственно, три значения суммарного напряжения.
1. Индуктивный характер напряжения. Соответствует случаю, когда 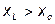 (рис. 3.14). При этом режиме угол
(рис. 3.14). При этом режиме угол 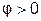 .
.
2.
 |
Емкостной характер напряжения. Соответствует случаю, когда
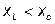 (рис. 3.15). При этом режиме
(рис. 3.15). При этом режиме 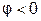 .
.
3. Резонанс напряжений. Соответствует случаю, когда 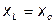 (рис. 3.16). При этом
(рис. 3.16). При этом 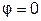 (см. подробнее раздел 3.10).
(см. подробнее раздел 3.10).
 |
Из формулы 3.41 можно сделать вывод, что мощности P, Q, S связаны следующей зависимостью:

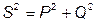 . (3.47)
. (3.47)
Графически эту связь можно представить в виде прямоугольного треугольника (рис. 3.17) – треугольника мощности, у которого имеются катет, равный Р, катет равный Q и гипотенуза S.
Отношение Р к S, равное 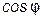 , называется коэффициентом мощности.
, называется коэффициентом мощности.
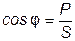 . (3.48)
. (3.48)
На практике всегда стремятся увеличить 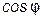 , так как реактивная мощность, которая всегда существует в цепи R, L, C, не потребляется, а используется лишь активная. Из этого можно сделать вывод, что реактивная мощность является лишней и ненужной.
, так как реактивная мощность, которая всегда существует в цепи R, L, C, не потребляется, а используется лишь активная. Из этого можно сделать вывод, что реактивная мощность является лишней и ненужной.
Дата добавления: 2015-03-26; просмотров: 1016;
