Методи розрахунку розмірних ланцюгів

Розв’язування задач з розмірними ланцюгами завжди складається з двох етапів: спочатку виявляють ланки, що входять у розмірний ланцюг і складають його умовну схему, а потім, вра ховуючи умову задачі, розв’язують її за допомогою математич­них методів. Перший етап роботи може бути складним і неодно­значним, особливо для багатоланкових просторових розмірних ланцюгів, до складу яких входять не тільки лінійні розміри де­талей, а й значення проміжків, натягів, ексцентриситетів, від­хилень форми, взаємного розміщення поверхонь тощо. Складальні розмірні ланцюги здебільшого є складнішими від детальних і отримують їх на підставі даних, взятих з багатьох робочих крес­лень (загального вигляду з усіма необхідними кресленнями вуз­лів і деталей).

Оцінюючи складність розмірного ланцюга, конструктор (тех­нолог, вимірювальник) часто з метою спрощення відповідальних розмірних ланцюгів вносить зміни у конструкції складових час­тин чи у способи позначення їх розмірів.

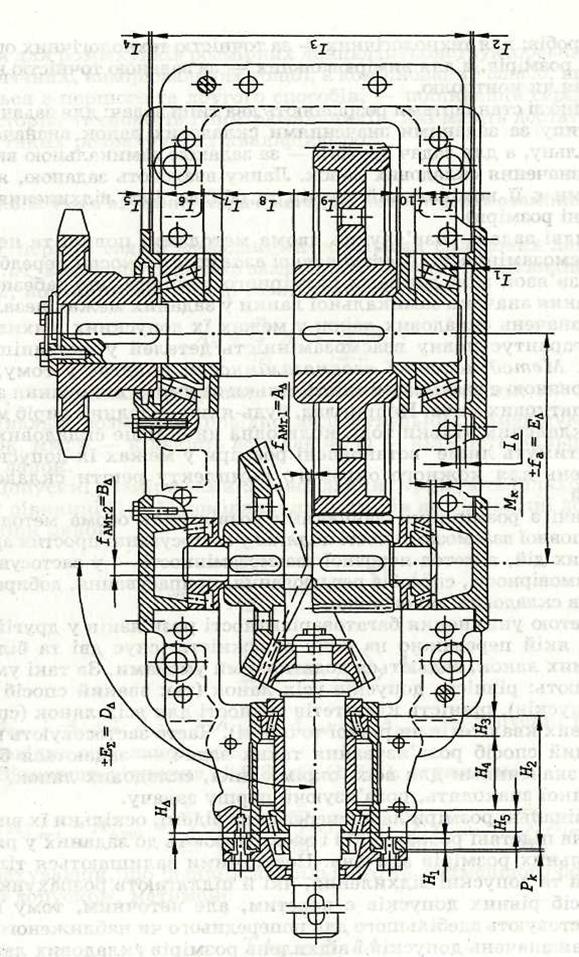
Як приклад для пошуку розмірних ланцюгів на рис 3.33 зо­бражено загальний вигляд відносно простої конструкції зубчастого редуктора. Пошук ланок будь-якого розмірного ланцюга почина­ють від замикальної ланки, задані розміри якої забезпечують за допомогою добору відповідних розмірів складальних ланок. Гра­ничні значення розмірів замикальних ланок розраховують чи при­значають відповідно до умов забезпечення якості виробу, тобто виконання ним встановлених функцій.

Як відомо, розмірний ланцюг є завжди замкненим колом, тому починаючи з будь-якого кінця розміру замикальної ланки послі­довно шукають усі розміри, які впливають на її значення, поки не прийдуть до другого її кінця, тобто замкнуть коло розмірів. На­приклад, розмірний ланцюг із замикальною ланкою J_Δ (рис. 3.33) містить 12 ланок, а розмірний ланцюг із замикальною ланкою Н_Δ складається з 6 ланок. Зазначені розмірні ланцюги, хоча й утворені багатьма ланками, однак пошук їх нескладний. Дещо складнішим є пошук розмірних ланцюгів для замикальних ла­нок, що забезпечують сходження ділильних конусів конічних зуб­частих коліс у одній точці по трьох взаємно перпендикулярних координатах, зміщення вершин ділильних конусів обох конічних коліс f_АМr відносно осей їх обертання, перетину цих осей, відхи­лень кута між осями ± Е_Σ, відстані між осями циліндричних зуб­частих коліс, їх паралельності f_х , перекошування f_y тощо. Пере­лічені розмірні ланцюги складаються як з лінійних, так і з куто­вих розмірів і є просторовими, тому спроектувавши всі ланки на заданий напрямок (переважно — напрямок замикальної ланки), їх зводять до лінійних розмірних ланцюгів.

Вимоги до точності замикальних ланок визначають: для конс­трукторських розмірних ланцюгів за функціональним призначен ням виробів; для технологічних — за точністю технологічних опера­ційних розмірів, а для вимірювальних — за заданою точністю вимі­рювання чи контролю.

Згідно зі стандартами розрізняють два типи задач: для задач пер­шого типу за заданими значеннями складових ланок визначають замикальну, а для задач другого — за заданою замикальною визна­чають значення складових ланок. Ланку вважають заданою, якщо відомими є її номінальний розмір та обидва його відхилення (чи граничні розміри).

Рис. 3.33. Розмірні ланцюги зубчастого редуктора

Обидві задачі розв'язують двома методами: повної та непов­ної взаємозамінності. Метод повної взаємозамінностіпередбачає такий зв'язок між ланками розмірного ланцюга, що забезпечує отримання значень замикальної ланки у заданих межах незалеж­но від значень складових ланок у межах їх допускних відхилень, тобто гарантує повну взаємозамінність деталей у складнішому виробі. Метод неповної взаємозамінностіполягає у тому, що гарантованою є взаємозамінність тільки за умови виконання зада­них додаткових умов. Наприклад, будь-який складний виріб може бути складеним тільки тоді, коли одна чи більше складових ла­нок матимуть лише встановлені розміри у межах їх допускних відхилень для кожного окремого комплекту решти складових деталей.

Задачі з розмірними ланцюгами розв'язують обома методами. Метод повної взаємозамінності (метод максимуму-мінімуму) полягає у застосуванні простих ариф­метичних дій, а метод неповної взаємозамінності — у застосуванні теорії ймовірності, способів регулювання, припасування, добирання розмірів складових ланок тощо.

Метод максимуму-мінімуму

У цій задачі за заданими розмірами складових ланок А₁, А₂, А₃,…, А_n визначають розмір замикальної ланки А_Δ. Як видно з рис. 3.32, номінальний розмір замикальної ланки

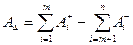,(3.1)

де А_Δ – номінальний розмір замикальної ланки, мм;

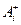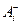і – номінальні розміри відповідно збільшувальних і зменшувальних ланок, мм;

n – кількість всіх ланок;

m – кількість збільшувальних ланок.

Допускні розміри замикальної ланки отримують шляхом заміни у рівнянні (3.1) номінальних розмірів на відповідні допускні розміри ланок

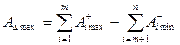, (3.2)

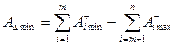, (3.3)

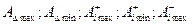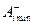де і – допускні розміри відповідно всіх ланок, мм.

Віднявши рівняння (3.3) від (3.2), отримаємо

,

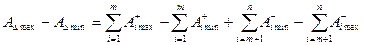а врахувавши, що різниця найбільшого та найменшого розміру є його допуском, матимемо

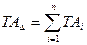,(3.4)

де 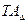і 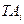– допуски розмірів відповідно замикальної та складових ланок, мм.

Віднімемо від рівнянь (3.2) і (3.3) рівняння (3.1) і врахуємо, що значення верхніх і нижніх відхилень розміру А такі:

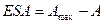;(3.5)

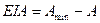,(3.6)

де ЕSA i EIA – відповідно верхнє та нижнє відхилення розміру А, мм;

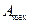і 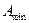– його допускні розміри, мм.

Після незначних перетворень отримаємо

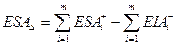; (3.7)

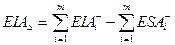, (3.8)

де 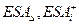і 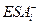– верхні відхилення розмірів відповідних ланок, мм;

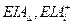і 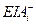– нижні відхилення розмірів відповідних ланок, мм.