Дисперсия оптической активности
Дисперсия оптической активности–это зависимость оптических характеристик вещества от длины волны падающего света. Чаще говорят о зависимости показателя преломления от длины волны и зависимости оптической активности от длины волны.
Дисперсия:
- нормальная, если показатель преломления убывает монотонно с ростом длины волны.
- аномальная, если показатель преломления изменяется резко.
Теория дисперсии оптической активности рассмотрена Кирквудом, а для спирали Моффитом.
Для обычных случаев оптической активности, когда эффект определяется асимметричными атомами углерода:
[m] = 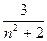
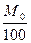 [α] =
[α] = 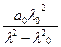 (формула Друде),
(формула Друде),
где 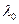 − полоса поглощения атомов, соседних с асимметричным атомом углерода (C
− полоса поглощения атомов, соседних с асимметричным атомом углерода (C 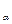 ).
).
На практике получается большое значение оптической активности.
Моффит получил выражение для дисперсии [m] макромолекул, содержащих спиральные участки:
[m] = 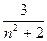
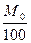 [α] =
[α] = 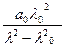 +
+ 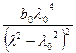 .
.
b0 – это коэффициент, пропорциональный содержанию α-спиральных структур.
b0 <0 для правых спиралей и положителен для левых.
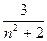 - множитель Лорентца, он характеризует влияние растворителя.
- множитель Лорентца, он характеризует влияние растворителя.
Часто вместо реальных полос берут эффективную полосу. Вблизи полосы поглощения оптическая активность становится очень большой, проходя через максимум, опускается, затем проходит через минимум. Резкое изменение оптической активности с сопровождающим круговым дихроизмом называется Коттон-эффектом. Измерение Коттон-эффекта в области 220–230 нм позволяет измерить характеристики вторичной структуры белков. Максимум при 230 нм характерен для всех белков, имеющих спиральную структуру. Величина максимума пропорциональна количеству спиральных областей.
3.29. Переходы “спираль-клубок”
Переходы “спираль-клубок” связаны с изменением конформации. Этот процесс происходит при изменении рН, ионной силы, состава растворителя. Эти процессы протекают кооперативно, и причины кооперативности связаны со структурой α-спирали или β-формы.
Конформации звеньев цепи взаимозависимы, т.к. водородная связь между i-ой и i−4-ой пептидной группировками накладывает жёсткие ограничения на конформации i−1-го, i−2-го и i−3-го звена. Для освобождения какой-либо пептидной единицы (а это означает выигрыш энтропии) необходимо одновременно разорвать как минимум три водородные связи кряду, а на это необходима определенная энергия. Поэтому пептидные звенья могут освобождаться только кооперативно.
Зимм и Бреггг разработали теорию перехода “спираль - клубок”, воспользовавшись моделью Изинга. Основная задача в их теории – это нахождение стат. суммы. Согласно этой теории рассматривается два типа состояний звеньев цепи:
1-ое состояние – это состояние связанного водородной связью звена− μi=1.
2-ое состояние − это состояние свободного звена − μi=0.
Свободная энергия цепи зависит от значений μi, причем непосредственно взаимозависимы конформации четырех последовательных звеньев:
F(μ1, μ2,…μN) = 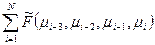 .
.
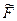 - это свободная энергия i-го звена, в котором учтена корреляция с предыдущими звеньями.
- это свободная энергия i-го звена, в котором учтена корреляция с предыдущими звеньями.
Считаем цепь очень длинной N >> 1 и пренебрегаем концевыми эффектами. Свободная энергия свободного звена не зависит от состояний предшествующих звеньев, т.е. Fсвоб. 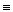
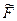 (μi-3, μi-2, μi-1, 0).
(μi-3, μi-2, μi-1, 0).
Свободная энергия связанного звена , следующего за связанным:
Fсвяз.. 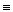
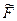 (μi-3, μi-2, 1, 1)
(μi-3, μi-2, 1, 1)
Свободная энергия связанного звена при такой записи не зависит от состояний i−3 и i−2, т.к. ограничения, которые накладываются предшествующим звеном (i−1), уже учли эту зависимость. Таким образом, изменение свободной энергии цепи при увеличении числа звеньев на единицу за счет соседнего несвязанного звена:
ΔF = Fсвяз. – Fсвободн. = 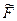 (μi-3, μi-2, 1, 1) -
(μi-3, μi-2, 1, 1) - 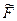 (μi-3, μi-2, μi-1, 0).
(μi-3, μi-2, μi-1, 0).
Если связанное звено появляется после трех свободных, то для этого нужна дополнительная энергия сверх ΔF. Связывание звена в этом случае означает инициирование спирали (возникновение) и она накладывает ограничения на четыре звена.
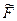 (0, 0, 0, 1) = Fсвяз. + Fиниц.
(0, 0, 0, 1) = Fсвяз. + Fиниц.
Свободная энергия инициации определяется уменьшением энтропии связываемых звеньев:
Fиниц = 4RTln3 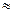 2,5
2,5 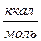 (при вращении свободного звена возможно возникновение трёх поворотных изомеров).
(при вращении свободного звена возможно возникновение трёх поворотных изомеров).
R = 2 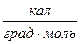 ; Т = 300 0К.
; Т = 300 0К.
Свободная энергия для освобождения одного или двух звеньев, заключенных между связанными звеньями, должна быть очень большой, т.к. звенья при этом остаются в спирали. Энергия, затрачиваемая на разрыв водородной связи, не компенсируются повышением энтропии, поэтому
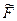 (μi-3, 1, 0, 1)
(μi-3, 1, 0, 1)  ,
,
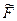 (1, 0, 0, 1)
(1, 0, 0, 1) 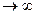 .
.
Зная эти значения для свободной энергии, запишем статистическую сумму, введя систему множителей:
1) 1 для каждого звена в свободном состоянии (μi=0).
2) S для звена в связанном состоянии (μi=1):
3)
S = e-ΔF/kT .
Физический смысл S – это константа равновесия для реакции образования водородной связи в звене, следующем за связанным.
4) σ – для каждого связанного звена, следующего за тремя и более свободными:
σ = е-Fиниц./кТ.
Физический смысл σ – это константа равновесия для реакции образования одного разрыва в последовательности водородных связей.
Для Fиниц. 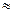 2,5
2,5 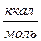 σ
σ 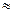 10-2.
10-2.
σ играет роль фактора кооперативности. Чем выше кооперативность процесса, тем меньше σ.
4) 0 для каждого связанного звена, следующего за одним или двумя несвязанными.
Все это приводит к тому, что можно записать стат. сумму:
Z= 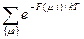 .
.
Зимм и Брегг показали, что задача упрощается, если ограничиться рассмотрением состояний всего лишь двух последующих звеньев:
F (μ1, μ2,…μN) = 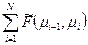 .
.
Fсвоб. = 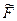 (μi-1, 0).
(μi-1, 0).
Fсвяз.. = 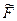 (1, 1).
(1, 1).
Fсвяз. + Fиниц = 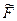 (0, 1).
(0, 1).
Считаем, что свободная энергия несвязанного звена равна нулю, для него множитель равен 1. Для каждого связанного звена – множитель S и для каждого первого из связанных звеньев, следующего за одним или большим числом свободных, множитель σ.
Z = 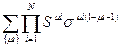 .
.
Z в виде суммы произведений можно представить как след матрицы (сумму диагональных элементов):
Z = Sp(pN) = λ1N + λ2N.
Характеристическое уравнение:
Z = (λ – 1)(λ – S) = σS.
Рассмотрим два крайних случая:
1) σ =0 – полная кооперативность (Fиниц 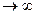 ):
):
λ1 = 1; λ2 = S
Z = 1+ SN
При N>> 1
Z = SN (S>1) или Z =1(S<1).
Видно, что переход “спираль - клубок”, осуществляется в точке S=1 и происходит по типу “все или ничего”.
Доля связанных пептидных единиц равна:
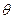 =
= 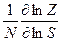
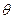 =
= 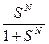 (
( 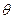 =
= 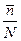 ; Z = 1+ SN) и при N >>1 θ = 1 (S>1) или θ = 0 (S<1).
; Z = 1+ SN) и при N >>1 θ = 1 (S>1) или θ = 0 (S<1).
Если σ мало, но не равно нулю, то решение характеристического уравнения дает переход не в одной точке, а в некотором интервале значений S. Этот интервал ΔS тем уже, чем меньше σ.
2) σ =1 - кооперативности нет(Fиниц=0):
(λ-1)(λ-S) = σS
λ1 = 1+S; λ2 = 0
Z = (1+ S)N , т.е. представляет собой произведение стат. сумм отдельных единиц. Это означает, что разрыв водородных связей в каждом звене происходит независимо. Доля связанных пептидных единиц равна:
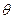 =
= 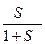 ;
;
Т.к S = e-ΔF/kT , то зависимость θ(S) одновременно является зависимостью θ(Т).
Плавлению спирали отвечает S = 1
Тплав = Тm = 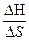 , где
, где 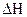 и
и 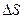 − разность энтальпии и энтропии клубка и спирали.
− разность энтальпии и энтропии клубка и спирали.
Расчеты показывают, что интервал значений ΔТ, в котором происходит плавление, оказывается:
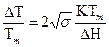 ;
;
3) промежуточный случай.
0 < σ < 1
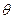 =
= 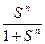
1 < n < N
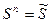 .
.
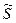 - константа равновесия для реакций, в которых одновременно участвуют n единиц.
- константа равновесия для реакций, в которых одновременно участвуют n единиц.
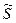 =
= 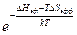 - это эффективные значения изменения энтропии и энтальпии, зависящие от n. Т.к
- это эффективные значения изменения энтропии и энтальпии, зависящие от n. Т.к 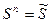 , то ΔHэф = Δhn. Δh – это изменение энтальпии при освобождении одного звена.
, то ΔHэф = Δhn. Δh – это изменение энтальпии при освобождении одного звена.
Когда: n=N, σ = 0
σ = 0, n = 1.
При N >> 1, Z = λ1N
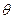 =
= 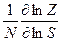 ≈
≈ 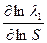 ≈
≈ 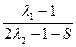 (1);
(1);
С другой стороны, 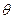 =
= 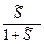 (2).
(2).
Приравняв (1) и (2) получим: 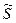 =
= 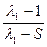
ΔHэф = 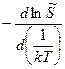 =
= 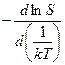
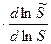 =
= 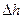
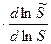 ;
;
S = 1
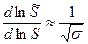
ΔHэф = Δhn
и n = 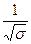 ;
;
Величину ΔHэф находят по углу наклона зависимости степени спиральности θ от 1/кТ и области перехода. Т.к. в этой области 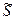 ≈1, то
≈1, то
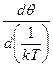 = −
= − 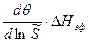 = −
= − 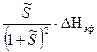 = −
= − 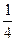
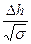 = −
= − 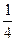 nΔh.
nΔh.
Параметры перехода “спираль - клубок” зависят от молекулярной массы, от условий эксперимента (рН, ионной силы), от гидрофобности и типа белка (состав, последовательность аминокислот).
Т.к. in vitro не определяются функциональные характеристики белков, то не следует такой процесс плавления белка в растворе называть денатурацией. Денатурация – это конформационное изменение биологической макромолекулы, приводящее к утрате ею способности к выполнению определенной биологической функции. Эта утрата может быть необратимой и обратимой. Процесс, обратный денатурации, называют ренатурацией. Когда речь идет о сложных белках и надмолекулярных комплексах, в которых участвуют белки, восстановление структуры по физико-химическим критериям – это недостаточное основание для суждения о восстановлении функциональной активности.
Дата добавления: 2015-02-07; просмотров: 6901;
