Устойчивость сжатых стержней

Физический смысл устойчивости Вы можете понять, проведя эксперимент. Возьмите тонкую гибкую линейку. Поставьте ее одним концом на стол, а на другой конец надавите рукой, увеличивая усилие. В начале линейка не изгибается (положение устойчивого равновесия), наступает момент, когда линейка, слегка изогнувшись, начинает «дышать» под вашей рукой (положение безразличного равновесия), при дальнейшем увеличении силы линейка резко изгибается (теряет устойчивость), это (положение неустойчивого равновесия).

Сила, при которой наступает безразличное равновесие, называется критической силой F_кр. Очевидно, что допускаемая нагрузка должна быть меньше критической силы

[F] = F_кр/ n_у, (1.15)

где n_у –коэффициент запаса устойчивости.

Рекомендуется: для стали n_у =1,8…3;для чугуна n_у = 5…5,5; для дерева n_у = 2,8…3,2. Однако, в зависимости от условий работы конструкции и от ее специфики, Вы можете увеличить этот коэффициент. Так для ходовых винтов металлорежущих станков принимают n_у = 4…5.

Критическая сила определяется по формуле

Рис.1.23Эйлера

F_кр = π²*Е*J_min/(μ*l)², (1.16)

где Е– модуль упругости; J_min – минимальный осевой момент инерции;

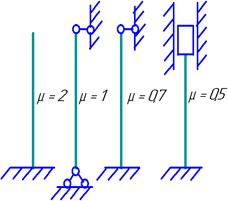
l – длина стержня; μ –коэффициент, зависящий от способа закрепления концов стержня (рис.1.23).

Напряжения в стержне при критической силе определяются зависимостью

σ _кр = F_кр/А = π²*Е*J_min/[(μ*l)²*А] =

= π²*Е/(μ*l/i_min)² = π²*Е/λ² ≤ σ _пц, (1.17)

где i_min = √ J_min/А – наименьший радиус инерции сечения стержня;

λ = μ*l/ i_min – гибкость стержня; σ _пц – предел пропорциональности материала стержня (см. диаграмма растяжения).

Из формулы (1.17) получаем λ ≥ π*√Е/ σ _пц – это условие применимости формулы Эйлера. Так для малоуглеродистой стали λ ≥100; для чугуна λ ≥80; для дерева λ ≥110; для легированных сталей λ ≥70.

В практике расчета строительных конструкций очень часто проводят подбор сечений сжатых стержней именно из условия устойчивости. При этом используется формула

[F] = φ* [σ _с]*А, (1.18)

где [σ _с] – допустимые напряжения на сжатие; φ – коэффициент, зависящий от материала и гибкости стержня (берется из таблиц). Из формулы (1.18) имеем

А = [F]/( φ* [σ _с]).

Коэффициентом φ задаются в первом приближении (обычно φ= 0,5), определяют А, выбирают профиль. Затем определяют гибкостьλ, уточняют φи снова находят А. Расчеты продолжают до получения оптимального соотношения устойчивости и прочности (обычно это 2 или 3 приближения).

В качестве примера проверим на устойчивость подкос (рис.1.7).

Дано:

F = Ν= 3510 Н; Е= 8*10⁴ МПа; l = b/Cos(35^о) =0,8/0,82 = 0,97 м;

А= 48 мм², соответственно d = 8 мм; [σ]= 74 МПа, μ = 1.

Решение:

Определим критическую силу

F_кр = π²*Е*J_min/(μ*l)² = 3,14²*2*10⁵*0,05*8⁴/(1*970²) = 429 Н < F =3510 Н.

Видим, что стержень диаметром 8 мм не выдерживает на устойчивость.

Возьмем обыкновенную водогазопроводную трубу 21,3х2,8 (труба с условным проходом 15мм). Площадь сечения трубы 162 мм² > А= 48 мм².

J_min = 0,05(D⁴ – d⁴) = 0,05*(21,3⁴ – 15,7⁴) = 7254 мм⁴.

F_кр = π²*Е*J_min/(μ*l)² = 3,14²*2*10⁵*7254/(1*970²) = 15203 Н > F =3510 Н.

Коэффициент запаса устойчивости n_у = F_кр/ F = 4,33.

Труба проходит по всем параметрам.

Вывод:при создании реальных конструкций не всегда достаточно расчета отдельных элементов по одному из видов деформаций, необходим всесторонний анализ конструкции и проверочный или проектировочный расчет по всем возможным видам деформаций если результат не очевиден.

Вот и закончен краткий курс сопротивления материалов. Надеюсь, его будет достаточно для решения большинства Ваших практических задач. Для тех, кто хочет расширить свои знания и решать задачи более сложные, чем мы рассмотрели, из очень обширного перечня рекомендую литературу, написанную (на мой взгляд) достаточно простым и понятным языком.

Литература

1. Степин П.А. Сопротивление материалов. 9-е изд.- М.: Интеграл-пресс, 1997. – 320с.

2. Феодосьев В.И. Сопротивление материалов. 10-е изд. – М.: Из-во МГТУ, 1999. – 590 с.

3. Беляев Н.М. Сопротивление материалов. 15-е изд. – М.: Наука, 1976. – 607 с.

4. Любошиц М.И., Ицкович Г.М. Справочник по сопротивлению материалов. – Минск: Вышэйшая школа, 1969. – 464 с.

5. Сборник задач по сопротивлению материалов / Под ред. А.А.Уманского. – М.: Наука, 1975. – 496 с.