Деформация растяжения и сжатия

Этот вид деформации показан на рис.1.5.

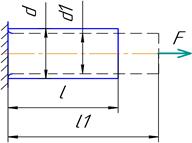Δl = l1- l – абсолютная продольная деформация.

Δd = d – d1 – абсолютная поперечная деформация.

ε = Δl/l – относительная продольная деформация.

ε¹ = Δd/d – относительная поперечная деформация.

Очевидно, что эти две деформации взаимосвязаны. Первым эту связь установил Пуассон.

Рис. 1.5

Запишем коэффициент Пуассона.

μ = ε¹/ ε = 0,25…0,33 ≈ const.

При растяжении или сжатии внутри стержня возникают только нормальные силы, а значит только нормальные напряжения. Поэтому можем записать условие прочности.

σ = Ν/Α ≤ [σ] - условие прочности при растяжении (сжатии) (1.2)

Между напряжением и относительной продольной деформацией существует зависимость, которую первым установил Гук. Запишем закон Гука.

σ = Е*ε (1.3)

- напряжение пропорционально относительной продольной деформации. Здесь Е– модуль упругости первого рода или просто модуль упругости.Он характеризует жесткость материала, то есть его способность сопротивляться деформированию.

Для стали Е = 2*10⁵ МПа.

Закон Гука можно записать и в другом виде. Подставив вместо σ = Ν/Α, а вместо ε = Δl/l, получим

Δl = Ν*l/( Е*Α) (1.4)

Формула (1.4) позволяет определить абсолютную продольную деформацию, то есть ответить на 3-й вопрос сопромата.