Механизм

Ведущие и ведомые звенья. Механизм является кинематической цепью, отли­чающейся определенностью движения всех звеньев относительно неподвижно­го звена—стойки. Звенья, на которые действуют движущие силы, называются ведущими, остальные — ведомыми. Сле­довательно, механизмом называется кинематическая цепь, у которой при за­данном движении одного или несколь­ких звеньев относительно звена, приня­того за стойку, остальные звенья со­вершают вполне определенные движения.

При кинематическом исследовании ме­ханизмов иногда удобнее движение задавать не ведущим звеньям, на кото­рые действуют движущие силы, а дру­гим. В этом случае такие звенья называются входными; последнее звено в ки­нематической цепи, движение которого является производным от положения входного звена, называется выходным. Степень подвижности. Количество ве­дущих звеньев соответствует степени подвижности механизма W, т. е. степени свободы его относительно стойки. Если число подвижных звеньев плоского ме­ханизма га, число кинематических пар пятого класса — р₅, четвертого клас­са — p₄ то число возможных движений несоединенных в пары звеньев будет Зn, число условий связи, налагаемых па­рами пятого класса,— 2р₅, парами четвертого класса — р₄ и, следовательно, степень подвижности механизма

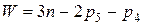. (1.2)

Формула (1.2) получила название фор­мулы Чебышева (по имени математика, впервые получившего ее в 1869 г.).

В тех случаях, когда рассматривают подвижность пространственного меха­низма, пользуются формулой Сомова — Малышева

W = ,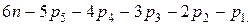

где р₁, р₂, р₃ — число пар первого, второго, третьего классов.

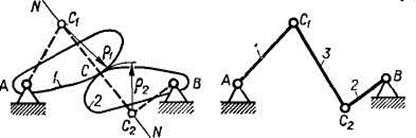Замена пар четвертого класса. Рас­пространенные методы изучения струк­туры механизмов разработаны для меха­низмов, в состав которых входят только низшие пары, поэтому при структурном анализе высшие пары (пары четвертого класса) условно заменяют кинемати­ческими цепями, содержащими лишь пары пятого класса. Заменяющие цепи, естественно, должны быть структурно и кинематически эквивалентны заменяе­мым парам. Простейшая заменяющая цепь (рис. 1.5) будет состоять из одного звена 3, расположенного на нормали NN к профилям звеньев 1 и 2, образу­ющих высшую кинематическую пару С. Длина звена 3 равна сумме радиусов кривизны р₁ и р₂. Это звено образует пары пятого класса С₁ и С₂ со звеньями 1 и 2.

Рис. 1.5 Замена высшей пары на цепь с низшими

Пассивные связи и лишние степени свободы.В формуле (1.2) не отражены размеры звеньев. Специальным подбо­ром размеров некоторых звеньев можно получить фактическую степень подвиж­ности, отличающуюся от подсчитывае­мой по формуле (1.2). Например, в механизме, показанном на рис. 1.6, а, при наличии звена EF степень под­вижности W = 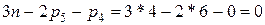, но если принять дополнительное условие, касающееся размеров звеньев, а именно АВ = = || CD = | EF (рис. 1.6, б), то, не­смотря на то, что по подсчету по-преж­нему

W = 0, фактически степень под­вижности W = 1 и механизм будет ра­ботать. При этих условиях звено EF можно исключить и степень подвиж­ности не изменится. Такие звенья, нали­чие которых не влияет на подвижность механизма, налагают пассивные или из­быточные условия связи и называются пассивными. В механизмы они вводятся < для увеличения жесткости, лучшего рас­пределения нагрузки, создания опре­деленности направления движения и т. д. Введение пассивных звеньев тре­бует высокой точности выполнения эле­ментов кинематических пар.

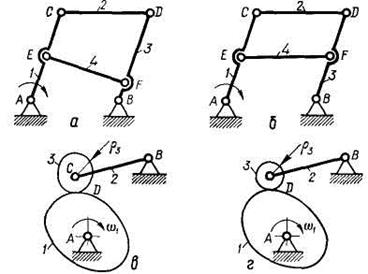В механизме, изображенном на рис. 1.6, в, W = . Вторую подвижность вносит звено 3 — некруглый ролик Ес­ли ролик сделать круглым (рис. 1.6, г), то характер относительного движения коромысла 2 будет таким же, как и в том случае, если ролик сделать непод­вижным. В этом смысле степень свободы, вносимая роликом, является «лишней». При закрепленном ролике п = 2; р₅ = 2;p₄=l;W = 3*2-

-2*2-1 = 1

Чаще всего звенья, создающие лиш­ние степени свободы, вводят в механизм для улучшения условий работы, повы­шения КПД (замена скольжения каче­нием) и т. д. При структурном анализе пассивные звенья и лишние степени свободы условно исключают.

Рис. 1.6. Шарнирные и кулачковые механизмы