Силы, действующие в механических системах
Силы тяжести звеньев при силовом анализе ферм и механизмов учитывают, если они велики по сравнению с другими действующими силами.
Равнодействующая сил тяжести звена Рв приложена в центре тяжести. Связь между силой тяжести (весом) Рв (кгс), массой звена т (кгс-с2/м) и ускорением земного притяжения g= 9,81 м/с2 выражается зависимостью
Рв = mg.
Центр тяжести сложной фигуры определяют как точку приложения равнодействующей сил тяжести простейших фигур, составляющих сложную .
Силы инерции звеньев нужно учитывать в большинстве современных механизмов, за исключением сравнительно тихоходных сильно нагруженных.
Для звена массы т, движущегося поступательно с ускорением а, равнодействующая сил инерции
Ри = — та
приложена к центру тяжести звена; линия ее действия параллельна направлению движения (рис. 3.1, а).
Пример 1. Определить, во сколько раз в двигателе автомобиля «Волга» сила инерции поршня Ри превышает его вес Рв при п = 4000 об/мин; r — 46 мм;
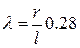 .
.
Решение. Наибольшее ускорение поршня (ползуна) (см. рис. 2.2)
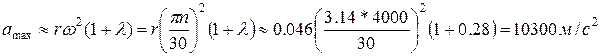 Искомое отношение сил
Искомое отношение сил 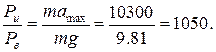
Для вращающихся звеньев, имеющих плоскость симметрии, перпендикулярную к оси вращения:
а) при ω = const и положении центра тяжести на оси вращения (rs = 0) силы инерции элементарных масс взаимно уравновешиваются (рис. 3.1, б);
б) при ω = const и 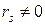 равнодействующая
равнодействующая 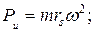
она приложена к центру тяжести и радиально направлена от оси, т. е. является центробежной силой (рис. 3.1, в);
в) при ω 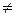 const и rs = 0 силы инерции приводятся к паре с моментом
const и rs = 0 силы инерции приводятся к паре с моментом
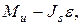
где Js = m 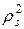 — момент инерции звена относительно центра тяжести; ps — радиус инерции звена; ε — угловое ускорение (рис. 3.1, г);
— момент инерции звена относительно центра тяжести; ps — радиус инерции звена; ε — угловое ускорение (рис. 3.1, г);
г) при ω 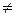 const и rs
const и rs 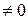 силы инерции приводятся (рис. 3.1, д) к равнодействующей
силы инерции приводятся (рис. 3.1, д) к равнодействующей 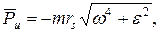
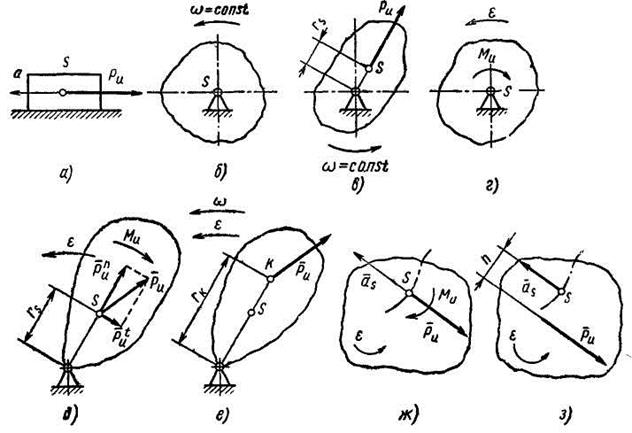 приложенной к центру тяжести звена, и к паре с моментом
приложенной к центру тяжести звена, и к паре с моментом 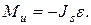
Рис. 3.1. Силы инерции, действующие на звенья:
а— движущееся , поступательно; б—е — вращающиеся; ж, з — совершающие сложное плоское движение
Нормальная и тангенциальная составляющие Ри:
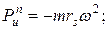
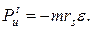
Ри и Ми могут быть также сведены к одной равнодействующей 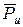 (рис. 3.1, е), приложенной в центре качания, который находится на радиальной прямой, проходящей через центр тяжести. Расстояние от оси вращения О до центра качания К
(рис. 3.1, е), приложенной в центре качания, который находится на радиальной прямой, проходящей через центр тяжести. Расстояние от оси вращения О до центра качания К 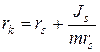 .
.
Для звеньев, совершающих сложное плоское движение, силы инерции приводятся к равнодействующей (рис. 3.1, ж)
Ри = — mas.
приложенной к центру тяжести, и к паре с моментом 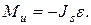 .
.
В приведенных формулах: as — ускорение центра тяжести звена; Js — момент инерции звена относительно оси, проходящей через центр тяжести перпендикулярно плоскости движения. Ри и Ми могут быть также сведены (рис. 3.1, в) к одной равнодействующей Ри = — mas, линия действия которой отстоит от центра тяжести звена на расстояние 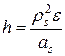 , где ps — радиус инерции звена, соответствующий Js.
, где ps — радиус инерции звена, соответствующий Js.
Моменты инерции полого цилиндра относительно осей x и y (рис. 3.2,а)
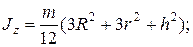
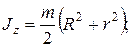
для сплошного цилиндра 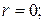 для боковой поверхости (тонкостенный элемент)
для боковой поверхости (тонкостенный элемент) 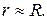
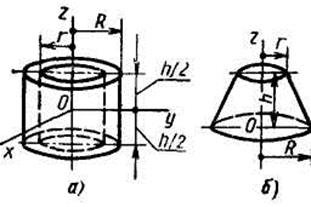 Момент инерции усечённого конуса (рис. 3.2,б)
Момент инерции усечённого конуса (рис. 3.2,б) 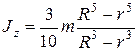 ;
;
для боковой поверхности усечённого конуса (тонкостенный элемент) 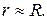
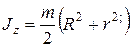
для целого конуса и его боковой поверхности 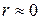 .
.
Рис. 3.2. К определению моментов инерции тел: а – цилиндрической формы; б – конической формы
Трение и силы трения.
Трением называется сопротивление относительному перемещению соприкасающихся тел, возникающее в месте их контакта. (рис.3.3)
Силы трения при сухом трении и трении со смазкой (полусухое, граничное, полужидкостное) определяются с помощью коэффициентов трения. Силы трения при жидкостном трении, когда трущиеся поверхности полностью разделены сло 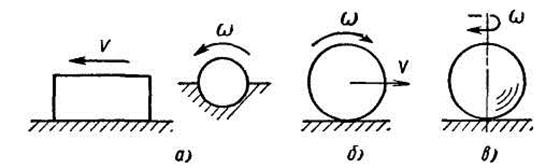 ем смазки, определяют по гидродинамической теории смазки.
ем смазки, определяют по гидродинамической теории смазки.
Рис. 3.3 Виды трения: а – скольжения; б – качения; в - верчения
Для уменьшения потерь на трение и снижения износа в кинематических парах применяют жидкостое трение вместо сухого, трение качения вместо трения скольжения.
Трение скольжения. (рис.3.4). Сила трения при движении
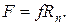
Предельная сила трения при покое (момент трогания с места)
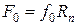 ,
,
где f и f0 –коэффициенты трения при движении и при покое в (табл. 3.1);
Rn - нормальная реакция.
Таблица 3.1. Ориентировочные значения коэффициентов трения
| Материалы трущихся тел | Коэффициент трения скольжения | Коэффи- циент трения качения движении к, см | ||||
| при покое fо | при движении f | |||||
| . без смазки | со смазкой | без смазки | со смазкой | |||
| Металл по металлу- | 0,15—0,3 | 0,1—0,2 | 0,15—0,2 | 0,05—0,2 | 0,001 — 0,005 | |
| Металл по дере- ву | 0,5 — 0,6 | 0,1—0,2 | 0,3—0,6 | 0,1—0,2 | ||
| 0,03—0,04 - | ||||||
| Дерево по дере- ву | 0,4—0,6 | 0,1 | 0.2—0,5 | 0,07— 0,15 | 0,05 — 0.08 | |
| Кожа по дереву | 0,4—0,8 | 0,3 — 0,5 | ||||
| Кожа по метал- лу | 0,3—0,5 | 0,15 | 0,6 | 0.15 |
 Более точные значения коэффициентов трения для конкретных условий приведены в специальной литературе (для фрикционных муфт, для тормозов, для пары колесо—рельс и т. д.).
Более точные значения коэффициентов трения для конкретных условий приведены в специальной литературе (для фрикционных муфт, для тормозов, для пары колесо—рельс и т. д.).
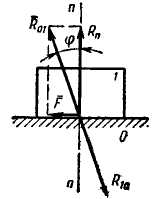
Угол трения φ — это угол между вектором полной реакции 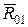 и нормалью к поверхности:
и нормалью к поверхности:
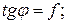
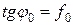 (рис. 3.4)
(рис. 3.4)
Рис. 3.4. Схема действия сил при трении скольжения и угол трения.
Обозначение реакций: 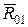 - сила, действующая от звена 0 на звено 1;
- сила, действующая от звена 0 на звено 1;
 - от звена 1 на звено 0.
- от звена 1 на звено 0.
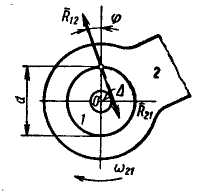 Круг трения радиуса
Круг трения радиуса 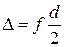 (рис. 3.5) характеризует трение во вращательной паре. Вследствие появления момента трения при вращении звена 2 относительно звена 1 линия действия реакций
(рис. 3.5) характеризует трение во вращательной паре. Вследствие появления момента трения при вращении звена 2 относительно звена 1 линия действия реакций 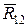 и
и 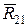 смещается относительно пары на
смещается относительно пары на 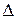 . Она должна быть касательной к кругу трения. Чтобы определить её направление пользуются следующим правилом: направление момента реакции (
. Она должна быть касательной к кругу трения. Чтобы определить её направление пользуются следующим правилом: направление момента реакции ( 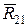 ) относительно центра О должно совпадать с направлением относительной угловой скорости с тем же индексом
) относительно центра О должно совпадать с направлением относительной угловой скорости с тем же индексом 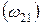 .
.
Рис. 3.5. Схема действия сил при трении скольжения во вращательной паре.
Приведенный коэффициент трения fпр позволяет привести сложный случай трения к простейшему случаю трения скольжения на горизонтальной плоскости, для которого
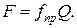
Приведенный угол трения определяется из выражения 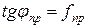 .
.
Некоторые значения 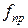 даны в табл. 3.2.
даны в табл. 3.2.
Трение качения. 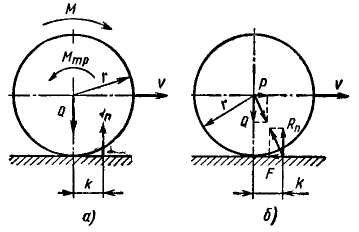 Момент трения, образованный парой сил Q= Rn при движении (рис. 3.6, а),
Момент трения, образованный парой сил Q= Rn при движении (рис. 3.6, а), 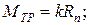
при покое в момент трогания с места 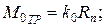
Сила трения при движении (рис. 3.6, б) 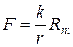
при покое в момент трогания с места
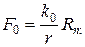
где k и k0 — коэффициенты трения качения при движении и при покое, имеющие линейную размерность, обычно см. (табл. 3.2).
Рис. 3.6. Схема действия сил и моментов при трении качения:
а – приложен движущий момент М; б – приложена движущая сила Р
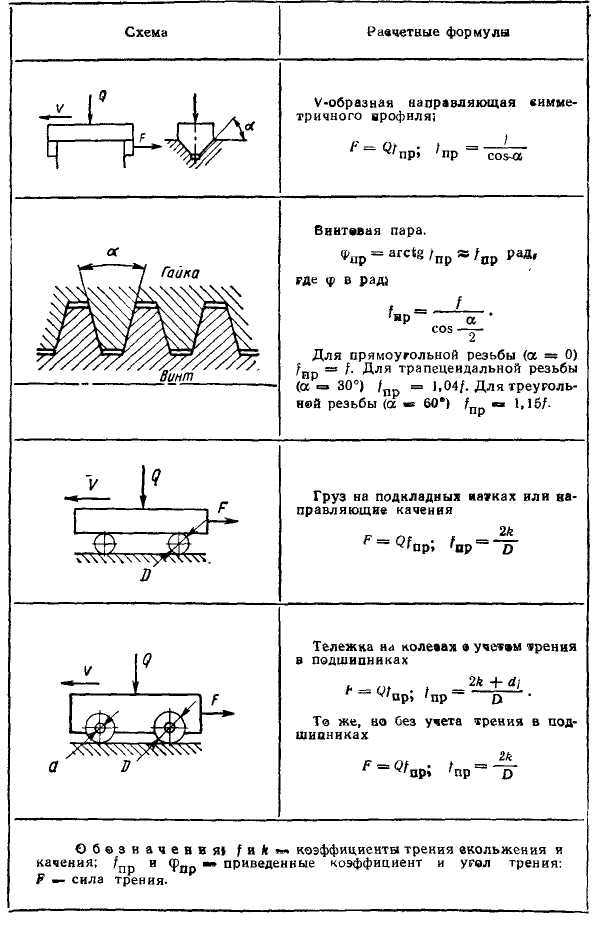 Табл. 3.2 Приведенные коэффициенты трения.
Табл. 3.2 Приведенные коэффициенты трения.
Дата добавления: 2015-02-05; просмотров: 1553;
