Кинематический анализ механизмов с низшими парами

2.1. Определение положений и перемещений звеньев

Графический метод. Положение звень­ев и траекторий точек определяется на кинематической схеме механизма.

Схема механизма, на которой зафик­сировано определенное положение веду­щего звена и в связи с ним положения всех остальных звеньев, называется пла­ном положения механизма. При вычер­чивании схемы механизма необходимо выбирать масштабы, соответствующие ГОСТ 2.302—88. Так как в дальнейшем при кинематических расчетах исполь­зуются величины, производные от дли­ны, то масштаб плана механизма должен иметь размерность [м/мм]. Рекомендуе­мые масштабы: 0,0001; 0,0002; (0,00025); 0,0005; 0,001; 0,002; (0,0025); 0,005; 0,01; 0,02 и т. д.

При вычерчивании плана положений механизма прежде всего нужно нанести положения неподвижных центров вра­щательных пар и направляющих посту­пательных пар. Затем для выбранного положения ведущего звена последова­тельно определяются положения кине­матических пар и звеньев групп, присое­диненных к ведущему звену.

Способ засечек. Определение положе­ний перемещающихся кинематических пар осуществляется способом засечек. В этом случае строится геометрическое место возможных положений центров вращательных пар (см. рис. 1.9, а). Из центров крайних кинематических пар (В и D) ближайшей к ведущему звену группы с помощью циркуля проводят дуги радиусами, равными 1вс и Idc, пересечение которых определит положе­ние центра внутренней вращательной пары С. Соединив полученную точку С прямыми линиями с точками В и D, находят положения звеньев ВС и CD. Таким же образом определяются поло­жения центров остальных кинематичес­ких пар.

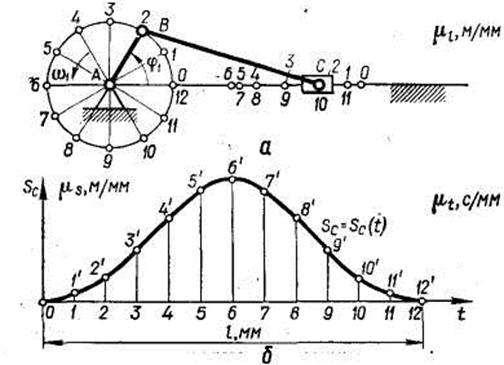
Рис. 2.1. К построению графика перемещений

Если необходимо проследить движе­ние определенной точки на каком-либо звене, следует отметить эту точку на каждом зафиксированном положении звена. Соединяя плавной кривой отме­ченные точки, получают траекторию дви­жения.

Метод графиков. Для представления о характере перемещений ведомого зве­на (рис. 2.1, а) пользуются графиками. На оси абсцисс графика (рис. 2.1, б)

в масштабе 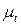(с/мм) откладывают вре­мя одного цикла (в период установив­шегося движения — это время, по исте­чении которого положение, скорость и ускорение звеньев механизма приобре­тают первоначальные значения). При выбранной длине отрезка на оси абс­цисс l, соответствующего времени одного цикла, и скорости ведущего звена, 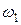масштаб 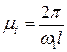(2.1)

По оси ординат откладывают линей­ное перемещение Sc ведомого звена в масштабе \is (м/мм) или угловое пере­мещение φ в масштабе μ_ф (рад/мм) для механизмов с вращающимся ведомым звеном.

В качестве начала отсчета удобно вы­брать одно из крайних положений ведо­мого звена; при этом кривая Sc = Sc (t), представляющая перемещение ведомого звена от этого крайнего положения, будет располагаться по одну сторону от оси абсцисс. Точность графического ме­тода определения перемещений невы­сока.

Аналитический метод. В тех случаях, когда необходимо получить высокую точность, применяют аналитические ме­тоды. Решения задачи аналитическим методом в общем случае сложны, так как зачастую приводят к громоздким вычислениям. Внедрение в практику ин­женерных расчетов цифровых ЭВМ поз­волило эту задачу упростить. При выборе способа аналитического исследо­вания выбирают такой, реализация ал­горитма которого на цифровых ЭВМ более проста. Наиболее удобным для этой цели является способ составления условия замкнутости всех закрытых кон­туров механизма, рассматриваемых как векторные многоугольники.

Исходными данными для реализации этого метода служат кинематическая схема, представленная в прямоугольной системе координат, линейные размеры всех звеньев и аналитическая зависи­мость изменения обобщенной координа­ты, определяющей положение ведущего звена.

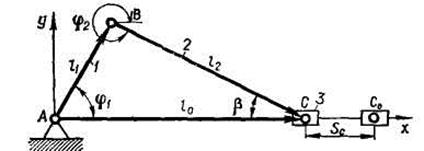
Рис. 2.2. К определению перемещения ползуна кривошипно-ползунного механизма

В качестве примера рассмотрим кривошипно-ползунный механизм. Кинематическая схема механизма (рис. 2.2) представляет собой замкнутый вектор­ный треугольник, уравнение замкну­тости которого

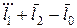= 0. (2.2)

Это условие можно также представить уравнениями проекций векторов на оси системы координат хАу (начало систе­мы координат находится на оси враще­ния кривошипа А) в виде

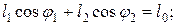
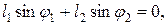(2.3)

где φ₁ , φ₂ — углы, образованные звень­ями 1 и 2 с осью Ах (рис. 2.2); l₁ l₂ — длины звеньев 1 и 2; l₀ = Хс — отстояние звена 3.

В этих уравнениях знаки при слага­емых определяются знаками тригоно­метрических функций.

В уравнениях (2.3) l₁ l₂ и угол пово­рота ведущего звена φ₁ известны, под­лежат определению величины φ₂ и Хс.

Используя геометрические соотноше­ния замкнутой цепи ABC и записав значение 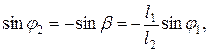(2.4)

можно получить положение ведомого звена в зависимости от угла φ₁ поворо­та кривошипа в виде Х_с , а обозначив 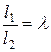, записать 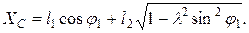(2.5)

Составив алгоритм и программу реа­лизации (например в Matcad) для соответствующего ПК, можно получить числовое решение с необходимой точностью.