Расчеты на прочность. Червячные передачи рассчитывают на прочность: по напряжениям изгиба и по контактным напряжениям

Червячные передачи рассчитывают на прочность: по напряжениям изгиба и по контактным напряжениям. В большинстве случаев прочность при изгибе не определяет размеры передачи и этот расчет применяют в качестве проверочного. В качестве проектного расчета на изгиб применяют только при больших числах зубьев колес (более 90 - 100) и для ручных передач. Основное значение имеет расчет по контактным напряжениям, который должен предотвращать в проектируемых передачах выкрашивание и заедание.

Условия зацепления и несущая способность передач с цилиндрическими червяками основных типов весьма близки, особенно при малом числе заходов. Поэтому расчеты, которые ведут в применении к передачам с архимедовым червяком, распространяются на передачи с другими цилиндрическими червяками.

Расчет на изгиб ведут по колесу, так как витки червяков значительно прочнее, и по номинальным напряжениям. Расчет аналогичен расчету косозубых цилиндрических колес только зубья червячных колес принимают на 20-40 % прочнее косозубых. Повышенная прочность зубьев червячных колес связана с их дуговой формой и с так называемой естественной коррекцией, имеющей место во всех сечениях, кроме среднего.

Напряжения изгиба зубьев

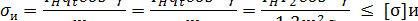
где 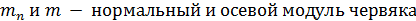; 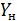- коэффициент прочности зубьев для червячных колес, выбираемый по эквивалентному числу зубьев 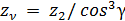; [σ]_и - допускаемое номинальное напряжение изгиба зубьев колеса, МПа. Множитель cos²γ учитывает наклон контактных линий и работу зуба как пластины.

Расчет по контактным напряжениям ведут по напряжениям в полюсе зацепления, которые не сильно отличаются от максимальных, но определяются проще, чем напряжения в других точках зацепления.

Аналогично расчету зубчатых передач в качестве исходной принимают известную формулу Герца для наибольших контактных напряжений при сжатии цилиндров вдоль образующих :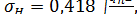

где Е – приведенный модуль упругости материала; ρ_ν – приведенный радиус кривизны.

Величина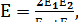

где Е₁ – модуль упругости материала червяка; Е₂ – модуль упругости материала колеса.

Витки архимедова червяка в средней плоскости имеют профиль прямобочной рейки ρ₂ = ∞, а зубья червячного колеса имеют эвольвентный профиль (рисунок 3.23); поэтому расчетный приведенный радиус кривизны равен радиусу кривизны зуба червячного колеса в полюсе зацепления, т. е.

.

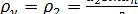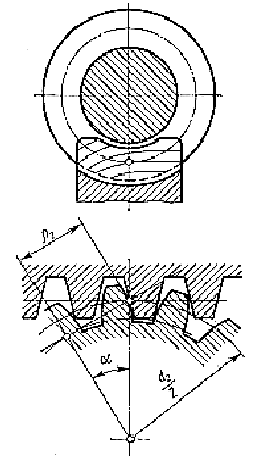
Рисунок 3.23 – Эвольвентный профиль

Подставив в исходную зависимость ρ_ν, а также q_n; Р₂; d₂ = mz₂; d₁ = mq; 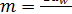; α = 20⁰; Е₁ = 2,15∙10⁶ кгс/см²; Е₂ = 0,9∙10⁶ кгс/см²(для бронзы и чугуна), после преобразований получазм формулу для [σ]_Н (МПа)

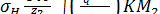≤ [σ]_Н