РАСЧЕТ ПРОЧНОСТИ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ПО НАКЛОННЫМ СЕЧЕНИЯМ

Построение условий прочности. При расчете прочности наклонных сечений исходят из условия, чтобы усилия от внешних нагрузок, действующие в наклонном сечении, были меньше или равны внутренним предельным усилиям в наклонном сечении. Усилия от внешних нагрузок представляют собой равнодействующую всех внешних сил (М и Q), расположенных по одну сторону от рассматриваемого наклонного сечения. Внутренние усилия в наклонном сечении определяются в предположении, что в этом сечении в предельном состоянии имеется наклонная трещина. Внутренние усилия в подобном наклонном сечении следующие:

– продольное и поперечное усилие в бетоне над наклонной трещиной;

– осевые и поперечные («нагельные») усилия в продольной арматуре, пересекающей наклонную трещину;

– осевые усилия в поперечной арматуре, пересекающей наклонную трещину;

– силы зацепления, действующие между берегами наклонной трещины.

Продольные и поперечные усилия в бетоне над наклонной трещиной представляют собой равнодействующие нормальных и касательных напряжений в нормальном сечении, проходящем через вершину наклонной трещины. Бетон в этой зоне работает в условиях сложного (неодноосного) напряженного состояния.

Продольная арматура, пересекающая наклонную трещину, в результате взаимного смещения берегов трещины удлиняется и изгибается. За счет этого в продольной арматуре возникают продольные усилия, моменты и поперечные усилия, определяемые соответственно осевыми напряжениями в арматуре, разностью краевых напряжений и приращением моментов по длине арматурного стержня. Однако напряжения в продольной арматуре к моменту разрушения сечения, как правило, не достигают своих предельных значений и не могут быть выражены через расчетные сопротивления арматуры.

Напряжения в большинстве стержней поперечной арматуры, пересекающей наклонную трещину, напротив, достигают предельных значений, т.е. расчетных сопротивлений. Поскольку в этих стержнях достигается предел текучести по всей площади стержня, то в арматуре действуют лишь осевые усилия, а поперечные, «нагельные», являются весьма незначительными.

Наконец, силы зацепления, действующие между берегами наклонной трещины, являются следствием взаимного смещения этих берегов. Дело в том, что наклонные трещины имеют, как правило, ломаную конфигурацию, а сама поверхность бетона в трещине является шероховатой. Поэтому при смещении соответствующих точек берегов наклонной трещины возникают силы зацепления впадин и выступов. Силы зацепления могут играть большую роль в работе сечения, особенно при отсутствии поперечной арматуры.

В процессе постепенного увеличения внешней нагрузки вначале образуется наклонная трещина. После этого при дальнейшем росте нагрузки напряжения в обоих видах арматуры (продольная и поперечная) и в бетоне над наклонной трещиной непрерывно увеличиваются. Расчетное сопротивление вначале достигается напряжениями в поперечной арматуре, а затем, в процессе текучести, наступает также предельное состояние либо бетона над наклонной трещиной, либо продольной арматуры. В первом случае разрушение бетона вызовет разрушение элемента в целом, хотя напряжения в продольной арматуре и не достигли предельных значений. Во втором случае нагрузка может расти и далее, пока не разрушится бетон над трещиной или не нарушится анкеровка продольной арматуры, находящейся под предельными напряжениями. Возможен и третий вариант разрушения – при значительном насыщении элемента поперечной арматуры она не может достичь своих предельных сопротивлений и элемент разрушается от раздавливания бетона в середине высоты элемента, между наклонными трещинами.

Условие прочности наклонного сечения по поперечной силе формулируется на основе следующих предпосылок:

а) поперечное усилие, воспринимаемое бетоном над наклонной трещиной, вычисляется в зависимости от расчетного сопротивления R_p, размеров элемента и угла наклона сечения;

б) усилия в поперечной арматуре всегда направлены вдоль стержней;

в) в расчет вводится вся пересекаемая наклонным сечением поперечная арматура с растягивающими напряжениями, равными R_{а х}

г) сопротивление продольной арматуры R_sA_s действию поперечной силы не учитывается.

Под поперечной арматурой понимают отогнутые стержни и хомуты (как поперечные стержни сварных каркасов, так и хомуты вязаных каркасов).

В соответствии с этим условие прочности, вытекающее из уравнения проекции усилий, имеет вид

Q ≤ ΣR_sω·A_sω + ΣR_sω·A_{sin c}sinα + Q_b

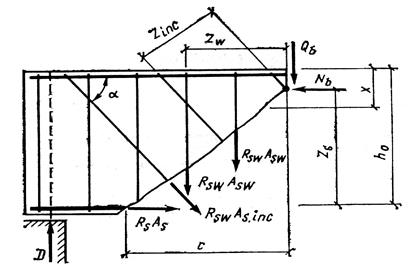где Q – поперечная сила, действующая в наклонном сечении, (равнодействующая поперечных сил от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения); ΣR_sω·A_sω; ΣR_sω·A_{sin c}sinα – сумма поперечных усилий, воспринимаемых соответственно хомутами и отогнутыми стержнями, пересекающими наклонным сечения; a – угол наклона отогнутых стержней к продольной оси элемента; Q_b – поперечное усилие, воспринимаемое бетоном сжатой зоны в наклонном сечении.