Расчет прочности на действие поперечной силы
Перед тем как приступить к расчету по поперечной силе, необходимо проверить два условия. Первое условие, определяющее необходимость расчета по поперечной силе, связано с возможностью образования наклонной трещины. Такая трещина не образуется и расчет на поперечную силу можно не производить, если
Q ≤ k1·Rbt·b·h0
где k1 – безразмерный эмпирический коэффициент; для тяжелого бетона 0,6 или 0,75 в случае соответственно балок и сплошных плоских плит.
Если окажется, что расчет на поперечную силу необходим, то нужно проверить второе условие для предельного значения поперечной силы, чтобы избежать раздавливания бетона между наклонными трещинами от действующих здесь наклонных сжимающих усилий:
Q ≤ 0,35 k1·Rbt·b·h0
Для бетона проектных марок выше В10 принимают как для класса В10.
Если условие соблюдается, то можно приступить к определению площади арматуры, воспринимающей поперечную силу.
Расчет элементов, армированных поперечными стержнями (хомутами) без отогнутых, стержней. Рассмотрим наиболее часто встречающийся в практике случай, когда элемент имеет только продольную арматуру и хомуты (без отгибов). Условие прочности элемента имеет вид
Q ≤ Qsωb
где Qsωb – предельная поперечная сила, воспринимаемая бетоном и хомутами в невыгеднейшем наклонном сечении
Qsωb= 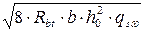
qsω – усилие в поперечных стержнях (хомутах) на единицу длины элемента,
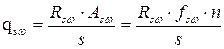
Длина проекции невыгоднейшего сечения определяется по формуле;

где s – шаг поперечных стержней (хомутов); fsω – сечение одного поперечного стержня (ветви хомута); n – число поперечных стержней (ветвей хомутов) в сечении элемента.
Из уравнения определяем qsω
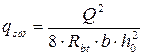
Интенсивность поперечного армирования должна быть не менее
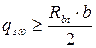
а назначаемый шаг поперечных стержней (хомутов) не должен превышать величины

Расчет прочности наклонных сечений на действие момента. Общее условие прочности наклонного сечения по изгибающему моменту записывают в виде уравнения.
МB ≤ Rs·As·zs+ ΣRsω· Asin c·zsinc + ΣRsω·Asω·zsω
При определенных конструктивных условиях это требование может быть выполнено, т. е. прочность балки на изгиб по наклонным сечениям будет обеспечена и расчет наклонных сечений можно не производить.
Конструктивные требования, обеспечивающие прочность балки на изгиб по наклонным сечениям, следующие:
1) при свободном опирании балки должна быть обеспечена анкеровка продольных стержней, доводимых до опоры; в этом случае условие прочности элемента на изгиб гарантируется не только в пролете, но и во всех наклонных сечениях, начинающихся у опоры;
2) для обеспечения анкеровки стержней продольной арматуры длина их запуска за грань свободной опоры должна составлять ls ≥ 5d если поперечная арматура по расчету не требуется; если же условие
Q ≤ 0,35 k1·Rbt·b·h0
не соблюдается, то ls ≥ 10·d ;
3) если анкеровка продольных стержней недостаточна, то предусматривают специальные конструктивные меры – приварку к концам стержней анкерующих пластин или закладных деталей, постановку косвенной арматуры в зоне анкеровки и т. п.
В целях экономии продольной арматуры часть ее (не более 50 %) в пролете можно уменьшать. Длина выпуска ω стержня за место обрыва может быть определена:
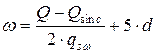
где Q – поперечная сила в точке теоретического обрыва стержня; Qsin с – поперечная сила, воспринимаемая отгибами (если они есть) в месте теоретического обрыва; qsω – усилие в хомутах на единицу длины балки на участке длиной ω; d – диаметр обрываемого стержня.
Величины Qsin и qsω определяют по формулам
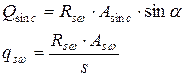
Дата добавления: 2015-02-03; просмотров: 4645;
