Пластический шарнир
Статически неопределимые балки и плиты железобетонных перекрытий рассчитывают с учетом перераспределения внутренних усилий, которое может происходить вследствие образования трещин, проявления неупругих свойств бетона и арматуры, а также частичного нарушения сцепления арматуры с бетоном. Это позволяет принять наиболее рациональную схему армирования элементов, а в ряде случаев снизить расход арматуры. Рассмотрим сущность такого расчета.
По мере увеличения внешней нагрузки напряжения в сечениях железобетонного элемента увеличиваются. Когда в наиболее напряженном сечении растянутая арматура достигает напряжений, равных пределу текучести, бетон сжатой зоны, имея высокие напряжения, испытывает значительные неупругие деформации. Такое напряженное состояние, возникшее в одном из сечений статически определимого элемента, приводит к повороту двух его частей (расположенных справа и слева от сечения), в результате которого напряжения в бетоне достигают временного сопротивления сжатию и наступает разрушение.
Если напряжения растянутой арматуры достигают предельных в каком-либо сечении статически неопределимого элемента, то разрушения в этом сечении не происходит, так как повороту примыкающих участков элемента препятствуют опорные закрепления, В рассматриваемом сечении происходят значительные местные деформации, но оно воспринимает момент
Мпл = σs·As·z
где As – площадь сечения арматуры; z – плечо внутренней пары сил.
Для расчета этот момент принимают равным:
Мпл = Rs·As·z
Участок балки, испытывающий указанное напряженное состояние, называют пластическим шарниром. При дальнейшем увеличении нагрузки на элемент момент в пластическом шарнире остается постоянным, а в других сечениях возрастает, т. е. происходит перераспределение моментов.
Пластические шарниры могут образовываться в нескольких сечениях элемента, до тех пор пока он не станет статически определимым, тогда образование еще одного пластического шарнира приведет к разрушению.
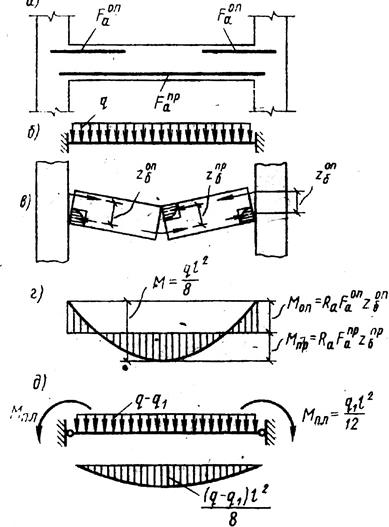
Для иллюстрации сказанного рассмотрим однопролетную статически неопределимую балку с защемленными концами пролетом l, загруженную равномерно распределенной нагрузкой q.
Предельные моменты, воспринимаемые пролетными и опорными сечениями балки, равны;
Мпл = σs·Asпр·zпр ; Моп = σs·Asоп·zоп
Сумма пролетного и опорного моментов в статически неопределимых балочных системах равна моменту свободно лежащей балки Мо:
При равномерно распределенной нагрузке
M0=q·l2 / 8
В рассматриваемом случае
σs·Asпр·zпр + σs·Asоп·zоп=q·l2 / 8
Задаваясь разными значениями Asпр и Asоп, мы получим соответственно различные значения пролетного и опорного моментов.
По упругому расчету такой балки опорные моменты Mоп=q·l2/12, а момент в середине пролета Mпр=q·l2 / 24 (Мпл + Моп =q·l2/8=Мо). Если количество арматуры, поставленное в опорных сечениях балки, будет меньшим, чем это требуется по указанной выше величине опорного момента, то в процессе загружения при нагрузке q1<q в опорных сечениях образуются пластические шарниры и дополнительная нагрузка (q-q1) вызовет увеличение моментов только в пролете. Так, если опорные сечения заармировать на момент Моп=q·l2/16, в пролете надо поставить арматуру на момент
Мпл = Моп -Мо =q·l2/8- q·l2/16= q·l2/16
Дата добавления: 2015-02-03; просмотров: 5561;
