Проектирование микрополосковой линии
Преимущества микрополосковой линии (рис. 1.1), как и симметричной полосковой, проявляются в полной мере в тех случаях, когда необходимо создать гибридные цепи, состоящие из элементов с сосредоточенными и распределенными параметрами. Всеми достоинствами, присущими симметричной полосковой линии, как и другие линии передачи, обладает в равной степени и микрополосковая линия, кроме одного. В микрополосковой линии существенно сильнее взаимное влияние между соседними проводниками, что обусловлено более открытой структурой линии и отсутствием симметрии относительно горизонтальной оси.
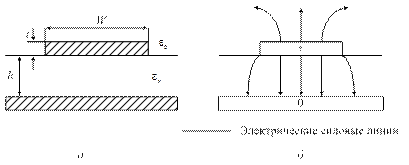
Рис. 1.1. Поперечное сечение(а) и структура поля (б) в микрополосковой линии
Как видно на рис. 1.1, конструкция микрополосковой линии чрезвычайно проста: металлический проводник (полоска) шириной W и толщиной t лежит на обеспечивающей прочность и жесткость конструкции подложке толщиной h, выполненной из однородного диэлектрика с относительной проницаемостью εr и покрытой с внешней стороны слоем металла. Структура поля в линии носит достаточно сложный характер. Теоретический анализ поля в микрополосковой линии усложняется тем, что лишь часть поля концентрируется в заполненном диэлектриком промежутке между полоской и заземленным проводником, а остальная – над и рядом с полоской в воздухе. Поэтому распространяющаяся в линии мода не чистая ТЕМ, а квази-ТЕМ. С помощью термина "квази-ТЕМ" подчеркивается, что различие в структуре полей, обусловленное присутствием в линии слоистой среды воздух (εr=1) – диэлектрик (εr≠1) этих двух мод, невелико. На низких частотах анализ, выполненный в предположении, что распространяется мода "квази-ТЕМ", дает вполне приемлемую погрешность, однако по мере повышения частоты становятся все более заметными продольные составляющие полей, что сказывается на результатах анализа. В частности, заметно проявляется дисперсия, т. е. волновое сопротивление линии и эффективная диэлектрическая проницаемость начинают зависеть от частоты.
При расчете микрополосковой линии возникает необходимость определять эффективную диэлектрическую проницаемость εэфф. Эта величина чрезвычайно полезна, т. к. характеризует соотношение между энергиями, концентрирующимися в воздухе и диэлектрике. Любая линия с модой ТЕМ характеризуется значением фазовой скорости νф. Напомним, что νф- скорость перемещения фронта волны вдоль линии: 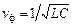 .
.
При отсутствии диэлектрического заполнения фазовая скорость в линии совпадает со скоростью света в свободном пространстве: 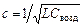 , где с≈3·108 м/с; L – погонная индуктивность линии с диэлектриком, равная в данном случае погонной индуктивности линии с воздушным заполнением; Cвозд – погонная емкость линии с воздушным заполнением; С – то же, но при наличии слоя из диэлектрика.
, где с≈3·108 м/с; L – погонная индуктивность линии с диэлектриком, равная в данном случае погонной индуктивности линии с воздушным заполнением; Cвозд – погонная емкость линии с воздушным заполнением; С – то же, но при наличии слоя из диэлектрика.
Из этих равенств следует 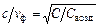 ,
,
т.е.
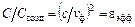 . (1.1)
. (1.1)
Микрополосковая линия с относительно широкой полоской (W/h → ∞) близка по своим свойствам к плоскому конденсатору, в котором практически вся энергия электрического поля концентрируется в диэлектрике под полоской. Поэтому значение εэфф вecьмa близко к значению εr. Ecли полоска узкая (W/h → ∞), то энергия электрического поля распределяется практически поровну между воздухом и диэлектриком. В этом случае значение εэфф близко к полусумме εr воздуха и диэлектрического слоя, т. е. εэфф ≈ (εr +1)/2. Следовательно:
(εr+l)/2 <εэфф < εr.
Для любой волны, распространяющейся в линии, фазовая скорость распространения с = ƒλ0 в свободном пространстве, vф = ƒλg при наличии диэлектрика.
Подставляя эти равенства в (1.1), получаем
εэфф=(λ0/λg)2, т. е.
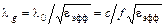 , (1.2)
, (1.2)
где λg – длина волны в микрополосковой линии.
В литературе приводится множество аналитических выражений для расчета параметров микрополосковых линий. Часть из них получена путем обработки результатов либо экспериментального исследования, либо, что чаще, – расчета на ЭВМ. Без таких аналитических выражений невозможно обойтись при машинном проектировании, когда требуется выполнить большое число расчетов с целью оптимизации конструкции. Наиболее общие выражения, пригодные для расчета микрополосковых линий с 0,05 <W/h< 20 при εr<16. При нулевой толщине полоски они имеют вид
для W/h < 1:
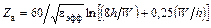 , (1.3а)
, (1.3а)
где 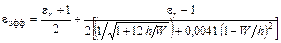 ;
;
для W/h ≥ 1:
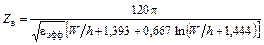 , (1.3б)
, (1.3б)
где 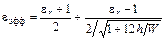 .
.
В указанном интервале изменения W/h и εr погрешность расчета значений Zв и εэфф по формулам (1.3) не превышает 1 %.
Для синтеза микрополосковой линии можно воспользоваться следующими выражениями:
при А< 1,52:
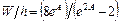 ; (1.4a)
; (1.4a)
при A ≥ 1,52:
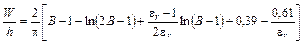 , (1.4б)
, (1.4б)
где 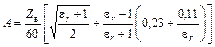 ;
; 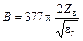 .
.
Погрешность расчета по (1.4) того же порядка, что и по (1.3). Влияние толщины полоски можно учесть, введя в (1.3) и (1.4) вместо физической ширины W полоски ее эффективную ширину Wэфф:
при W/h >1/2π:
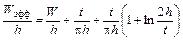 ; (1.5а)
; (1.5а)
при W/h <1/2π:
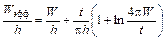 . (1.5б)
. (1.5б)
При записи (1.5) предполагалось, что t < h; t < W/2.
На частотах до 10 ГГц дисперсия эффективной диэлектрической проницаемости в микрополосковой линии обычно настолько мала, что ею можно пренебречь.
Волновое сопротивление микрополосковых линий, изготавливаемых промышленностью, обычно не выше 125 Ом и не ниже 20 Ом. Снизу значения Zв ограничиваются потерями на излучение и преобразованием в моды, распространяющиеся в поперечной плоскости линии. В качестве материала, из которого выполняется подложка, можно использовать разнообразные диэлектрики. Из них только два получили широкое применение на частотах до 18 ГГц и выше.
1. Неорганический диэлектрик на основе оксида алюминия с относительной проницаемостью 8 - 10 и содержанием чистого окисида алюминия до 99,5 %.
2. Органические диэлектрики типа полистирола или стеклотекстолита с относительной проницаемостью 2-3, используемые при разработке и моделировании полосковых устройств.
Отметим, что устройства на неорганической подложке можно разработать, предварительно изготовив эти устройства на органической подложке и, наоборот, с соответствующей коррекцией размеров всех цепей. При переходе с органической на неорганическую подложку все размеры следует уменьшить, т. к. относительная, следовательно, и эффективная диэлектрическая проницаемости возрастают [см. равенство (1.2)].
Так как толщина подложки микрополосковых плат невелика, вводят дополнительный металлический кожух, обеспечивая тем самым механическую жесткость, возможность отвода теплоты от активных элементов и защиту от атмосферного воздействия. Однако введение кожуха оказывает влияние на параметры линии, описываемые выражениями (1.3) - (1.5). Кожух экранирует внутреннее пространство от внешних полей. Внутри кожуха часть краевых полей замыкается на экран, а не рассеивается во внешнем пространстве, что приводит к увеличению напряженности полей в воздушном зазоре между кожухом и линией. Когда крышка и боковые части металлического кожуха удалены на расстояние, приблизительно в пять или шесть раз большее, чем соответственно толщина подложки и ширина полоски, влияние экрана на параметры линии, описываемые (1.3) - (1.5), пренебрежимо мало (табл. 1).
Для приближенного анализа и синтеза микрополосковой линии можно воспользоваться графиками на рис. 1.2, построенными с помощью (1.3) и (1.4).
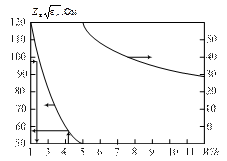 |
Рис. 1.2. Зависимость волнового сопротивления от W/h для
микрополосковой линии с полоской бесконечно малой толщины
Таблица 1
| Волновое сопротивление, Ом | ||
| er | ||
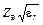
| ||
| Отношение W/h | 1,6 |
Дата добавления: 2015-02-03; просмотров: 5636;
