Способы корректировки автокорреляции (авторегрессионные модели первого порядка).

Одним из наиболее простых способов учета автокорреляции являются авторегрессионные модели различных порядков. Порядок авторегрессионной модели определяется максимальной величиной лага (m) случайного возмущения, включенного в спецификацию. Рассмотрим авторегрессионную модель первого порядка, в которой значение возмущения 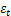, определяется через его лаговое значение первого порядка. В этом случае спецификация регрессионной модели с авторегрессией случайного возмущения принимает вид:

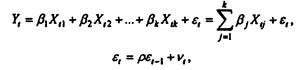где v_t, t = 1,...,n —случайные возмущения авторегрессионного уравнения — независимые нормально распределенные случайные величины: v_t,~ N(0, );

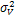ρ — коэффициент авторегрессии (параметр модели) (-1 < ρ < 1):

ρ > 0 — положительная автокорреляция; ρ < 0 — отрицательная автокорреляция; ρ = 0 — автокорреляции нет, удовлетворяется третье условие Гаусса—Маркова.

Необходимо определить начальные условия модели. Начальные условия модели определяются нормальной случайной величиной ε_t ~ N(0, 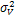) , где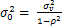

Корректирующий множитель ( 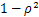)^-1 служит для обеспечения гомоскедастичности случайных возмущений. Покажем это. Определим элементы автоковариационной матрицы возмущений.

Диагональные элементы:

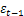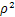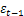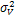Cov{e„e,} = Var{ ε_t } = Var{ρ + v_t }= Var { } + , t = 1,....,n. При t=1

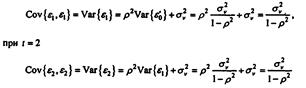и т. д., таким образом, для любого момента времени t дисперсия возмущения не зависит от времени:

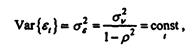т. е. задание дисперсии возмущения в начальном условии в виде обеспечивает гомоскедастичность случайному возмущению модели.

Данное выражение получено с учетом того, что случайные величины 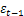и v_t независимы.

Недиагональные элементы, ковариации между значениями случайных возмущений, разделенными лагом: Cov{ 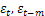}, m = 1,..., (n -1).

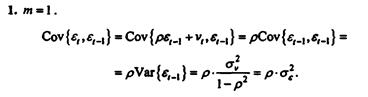Данное выражение получено с учетом того, что случайные величины 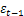и v_t независимы. Из полученного выражения ковариации (m = 1), в частности, следует, что

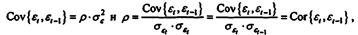т. е. параметр авторегрессии представляет собой коэффициент корреляции между возмущениями соседних наблюдений (с учетом гомосксдастичности случайного возмущения).

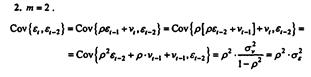и т. д. Таким образом, для любого лага автоковариационная функция процесса не зависит от момента t, а зависит только от величины лага m: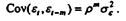

В теории случайных процессов процессы с ковариационными матрицами, обладающими таким свойством, называются стационарными случайными процессами.

48. Способы корректировки автокорреляции: алгоритм метода Кохрейна-Оркатта.

1. По выборочным данным выполняется настройка модели, и вычисляется вектор остатков регрессии е = (e₁, e₂ , …, e_n)^T.

2. По остаткам регрессии оценивается модель авторегрессии e_t=ρe_t-1+ v_t

3. С оценкой параметра авторегрессии выполняются этап преобразования переменных и определения МНК – оценок вектора параметра β.

4. Строится новый вектор остатков, и процедура повторяется, начиная с п. 2. Интеграционный процесс заканчивается при условии совпадения оценок по последней и предпоследней интерациях с заданной степенью точности.