Последствия автокорреляции случайного возмущения.

Последствия автокорреляции: при наличии автокорреляции МНК обеспечивает несмещенные оценки параметров, так как первая предпосылка Гаусса-Марков выполняется, 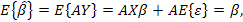но оценка дисперсии возмущения смещенная, .

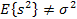Таким образом, числовыми характеристиками вектора остатков в условиях автокорреляции являются:

· ,

·

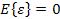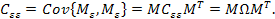
В этом случае 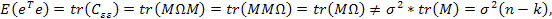что приводит к нарушению свойства несмещенности оценки дисперсии возмущения.

Смещенность оценки дисперсии возмущений приводит к неадекватным оценкам:

· автоковариационной матрицы оценок параметров

;

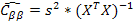· границ доверительных интервалов параметров модели и значений эндогенной переменной.

46. Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений.

Большинство тестов на наличие корреляции по времени в ошибках системы используют следующую идею: если корреляция есть у ошибок ε, то она присутствует и в остатках е, получаемых после применения обычного МНК. Пусть нулевая гипотеза состоит в отсутствие корреляции, то есть 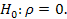В качестве альтернативной может выступать либо просто H₁: ‹‹не H₀››, либо односторонняя гипотеза, например H₁: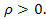

Широкое применение получил тест Дарбина-Уотсона. Тест основан на вычислении статистики DW:

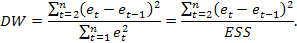
Предпосылки теста: случайные возмущения распределены по нормальному закону и гомоскедастичны. Поскольку коэффициент корреляции принимает значения 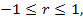то для значений статистики DW выполняется неравенство 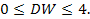Вычисленное значение статистики DW не сравнивается с ее критическим значение, так как его невозможно затабулировать в силу зависимости от значений регрессоров. Границы d_U и d_L выбираются из таблиц Дарбина-Уотсона по числу наблюдения n, числу регрессоров K и уровню значимости α.

Значение статистики DW	Вывод
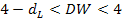
	Гипотеза H0 отвергается, есть отрицательная корреляция
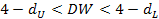
	Неопределенность
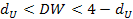
	Гипотеза H0 не отвергается
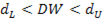
	Неопределенность
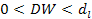
	Гипотеза H0 отвергается, есть положительная корреляция

Множество возможных значений статистики DW можно представить в виде следующих пяти интервалов на числовой оси:

Алгоритм теста Дарбина-Уотсона

1. Настройка модели и вычисление остатков.

2. Вычисление статистики DW

3. Выбор табличных значений границ критического значения статистики: d_U и d_L (по параметрам n,K,α).

4. Определение интервала, в который попадает вычисленное значение статистики DW.