Функция Лейбензона

При установившейся фильтрации сжимаемой жидкости и газа массовый расход во всех поперечных сечениях пласта одинаков

Q_m = const (4.72)

а объёмный расход возрастает по мере падения давления за счёт расширения жидкости или газа.

Назовём функцию

Р = ∫ ρdp + C (4.73)

функцией Л. С. Лейбензона.

Целесообразность введения этой функции видна из сопоставления формул, выражающих закон Дарси в дифференциальной форме для несжимаемой жидкости

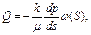(4.74)

где Q – постоянный объёмный расход жидкости, и для сжимаемой жидкости или газа

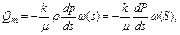(4.75)

где Q_m – постоянный массовый расход; dP = ρdp – дифференциал функции Лейбензона.

Выражение (4.74) и (4.75) являются однотипными дифференциальными уравнениями, в которых объёмному расходу Q в уравнении (4.74) соответствует массовый расход Q_m в формуле (4.75), а давлению в (4.74) – функция Лейбензона в (4.75).

Отсюда следует вывод, что все формулы, полученные для установившейся фильтрации несжимаемой жидкости по закону Дарси, можно использовать при установившейся фильтрации сжимаемой жидкости и газа при тех же граничных условиях со следующими переменными: